Алгебраические выражения

Алгебраическое выражение это запись, составленная со смыслом, в которой числа могут быть обозначены и буквами, и цифрами. Также она может содержать знаки арифметических действий и скобки.

Любую букву, обозначающую число, и любое число, изображённое с помощью цифр, принято считать в алгебре также алгебраическим выражением.

Алгебраические выражения, входящие в состав формул, могут применяться к решению частных арифметических задач, если в них заменить буквы данными числами и произвести указанные действия. Число, которое получится, если взять вместо букв какие-либо числа и произвести над ними указанные действия, называется численной величиной алгебраического выражения. Из этого легко сделать вывод, что одно и то же алгебраическое выражение при различных значениях входящих в него букв может иметь различные числовые величины.

Примеры:

1) Выражение

am + bn,

при a = 2, m = 5, b = 1, n = 4 вычисляется:

2 &middot, 5 + 1 &middot, 4 = 14,

а при a = 3, m = 4, b = 5, n = 1 вычисляется:

3 &middot, 4 + 5 &middot, 1 = 17 и т. д.

2) Выражение

abс,

при a = 1, b = 2, c = 3 равно:

1 &middot, 2 &middot, 3 = 6,

а при a = 2, b = 3, c = 4 равно:

2 &middot, 3 &middot, 4 = 24 и т. д.

Коэффициент

Коэффициент это числовой множитель алгебраического выражения, представляющего собой произведение нескольких сомножителей. Коэффициент в выражении ставится перед всеми остальными буквенными множителями. Таким образом,

произведение чисел a, b, c, d, 4 записывается так: 4abcd,

произведение чисел m, n, , p записывается так: .

Числа 4 и это коэффициенты. Очевидно, что

4abcd = abcd + abcd + abcd + abcd

и точно также

.

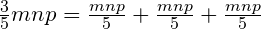Итак, коэффициент показывает, сколько раз целое алгебраическое выражение или известная его часть берется слагаемым.

Если в алгебраическом выражении нет числового множителя, то подразумевается, что коэффициент равен единице, так как

a = 1 &middot, a, bc = 1 &middot, bc

и так далее.

Виды выражений

Алгебраическое выражение, в которое не входят буквенные делители, называется целым, в противном случае дробным или алгебраической дробью.

Пример.

Целые алгебраические выражения:

7a2b, a2 +	2	bc .
	3

Дробные алгебраические выражения:

a2	,	m — n
b3		m + n	.

Выражения, не содержащие корней, называются рациональными, а содержащие корни иррациональными или радикальными. Например, все выражения, приведённые выше, являющиеся целыми или дробными, так же можно назвать и рациональными.

a , 53c + amn иррациональные или радикальные выражения.