Биквадратное уравнение уравнение, которое можно привести к виду:
ax4 + bx2 + c = 0,
где a &ne, 0.
Для решения биквадратных уравнений x2 заменяется на любую другую букву, например, на y, то есть:
если x2 = y, то ax4 + bx2 + c = ay2 + by + c = 0.
Следовательно, относительно y, уравнение является квадратным и решается по формуле корней квадратного уравнения, а затем вычисляются корни биквадратного уравнения, если они есть.
Пример. Решить уравнение:
x4 — 10×2 + 9 = 0.
Решение: Заменяем x2 на y, чтобы получить квадратное уравнение:
y2 — 10y + 9 = 0.
Вычисляем дискриминант:
D = b2 — 4ac = (-10)2 — 4 ·, 1 ·, 9 = 100 — 36 = 64, D >, 0.
Находим корни:
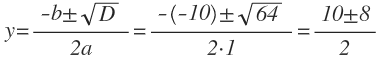
y1 = (10 + 8) : 2 = 9,
y2 = (10 — 8) : 2 = 1.
Теперь надо решить уравнения:
x2 = 9 и x2 = 1.
1) x2 = 9, x1 = 3, x2 = -3,
2) x2 = 1, x3 = 1, x4 = -1.
Ответ: 3, -3, 1, -1.