Дискриминант квадратного уравнения это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.
| Вид уравнения | Формула корней | Формула дискриминанта |
|---|---|---|
| ax2 + bx + c = 0 | 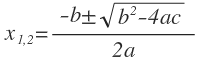 | b2 — 4ac |
| ax2 + 2kx + c = 0 | 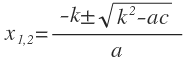 | k2 — ac |
| x2 + px + q = 0 | 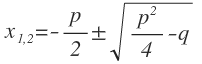 | 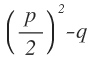 |
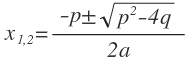 | p2 — 4q |
Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:
| Вид уравнения | Формула |
|---|---|
| ax2 + bx + c = 0 | 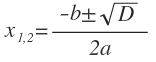 , где D = b2 — 4ac , где D = b2 — 4ac |
| ax2 + 2kx + c = 0 | 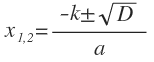 , где D = k2 — ac , где D = k2 — ac |
| x2 + px + q = 0 | 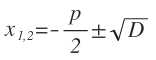 , где D = , где D = 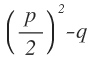 |
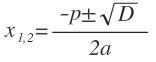 , где D = p2 — 4q , где D = p2 — 4q |
Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:
- Если дискриминант больше нуля, то уравнение имеет два корня.
- Если дискриминант равен нулю, то уравнение имеет один корень.
- Если дискриминант меньше нуля, то уравнение не имеет корней.
Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:
D = b2 — 4ac,
так как она относится к формуле:
 ,
,
которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.
Решение квадратных уравнений через дискриминант
Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.
Пример 1. Решить уравнение:
3×2 — 4x + 2 = 0.
Определим, чему равны коэффициенты:
a = 3, b = -4, c = 2.
Найдём дискриминант:
D = b2 — 4ac = (-4)2 — 4 ·, 3 ·, 2 = 16 — 24 = -8,
D <, 0.
Ответ: корней нет.
Пример 2.
x2 — 6x + 9 = 0.
Определим, чему равны коэффициенты:
a = 1, b = -6, c = 9.
Найдём дискриминант:
D = b2 — 4ac = (-6)2 — 4 ·, 1 ·, 9 = 36 — 36 = 0,
D = 0.
Уравнение имеет всего один корень:
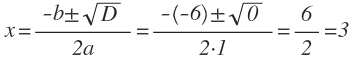
Ответ: 3.
Пример 3.
x2 — 4x — 5 = 0.
Определим, чему равны коэффициенты:
a = 1, b = -4, c = -5
Найдём дискриминант:
D = b2 — 4ac = (-4)2 — 4 ·, 1 ·, (-5) = 16 + 20 = 36,
D >, 0.
Уравнение имеет два корня:
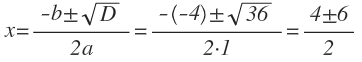
x1 = (4 + 6) : 2 = 5,
x2 = (4 — 6) : 2 = -1.
Ответ: 5, -1.