Квадратные уравнения не только математическая абстракция, но и вполне реальный инструмент решения прикладных вопросов. Форму стандартной записи уравнения имеет зависимость перемещения от скорости и времени, описание движение тела по дуге. Нельзя построить здание, если не использовать это выражение при архитектурных расчетах. Всюду, где имеет место квадратическая зависимость одной величины от другой, легко использовать алгоритм для расчета процессов.
Это заметили еще в древние времена. Неполные квадратные уравнения и примеры с решением были записаны в древнеиндийских и арабских трактатах. Оригинальные способы решения полных квадратных уравнений описаны в арабских книгах и вавилонских табличках. Арабский математик Аль Хорезми описывает целых шесть уравнений с неизвестным во второй степени. Современная запись и формула корней квадратного уравнения оформилась в середине 17 столетия и остается практически неизменной до наших дней.
Формула квадратного уравнения в общем виде выглядит так:
ах²+bх+с=0.
Необходимо уточнить, что в уравнении только одна переменная, это Х. Уточнение нужно по той причине, что многие ученики (и даже студенты) на вопрос, сколько переменных в квадратном уравнении, без малейшего сомнения отвечают, что две. На самом деле переменная одна, но только один раз записана в квадрате, второй раз, — в первой степени. Такая формула называется приведенным, или стандартным видом.
Если в первой степени не представлен (b= нулю) то уравнение принимает вид:
ах²+с=0.
Это тоже квадратное уравнение, но называется неполным. Еще одна запись:
ах²+bх =0.
В этом случае нулю равен коэффициент С.
Если уравнение приняло вид:
bх+с=0,
это не квадратное, а линейное уравнение.
Правильный ответ на вопрос, что такое квадратное уравнение может быть таким:
Любое уравнение, где переменная х находится во второй степени (квадрате).
Анализируем уравнение дальше. Коэффициенты а, b и с — целые числа. Они имеют свое название:
- коэффициент а – главный,
- b – второй, или коэффициент при х,
- с – свободный член.
На значение главного коэффициента налагается ограничение а≠ 0.
Корнем называется значение переменной, которое превращает уравнение в равенство 0=0. Корнем уравнения может быть любое число, от минус до плюс бесконечности, включая дробные. Есть уравнения, у которых в принципе нет решений. Если доказать, что корней нет, то это тоже представляется, как решение задачи.
Исторически сложилось так, что математики сначала нашли способы решения неполных уравнений. Рассмотрим выражение, записанное в форме ах²+с=0. То есть, второй коэффициент равен 0.
Перепишем уравнение в виде ах² = с.
Отсюда следует: ![]()
Очевидно, что а/-с ≥ 0. Это возможно в двух случаях:
- если в первоначальной записи а- положительное, с -отрицательное числа:
- если а- отрицательное, а с – положительное.
Для уравнения ах²+bх=0 схема решения тоже несложная:
ах²+bх=0,
х(ах+b)=0,
<,=>,
х=0,
ах+b=0,
х=0,
х=-b/а.
Самое простое уравнение ах²=0, если b=0, с=0. Решение выглядит так:
ах²=0,
х²=0,
х=0, при любом значении а.
Для начала необходимо привести уравнение в стандартный вид иногда для этого нужно выполнить ряд алгебраических преобразований. Допустим, что они сделаны и у нас есть уравнение вида ax2 + bx +c= 0, а≠ 0.
Для решения используем готовые формулы:
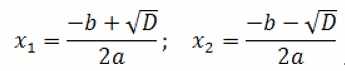
Обратим внимание на букву D под знаком радикала. Это выражение называют дискриминант. Он вычисляется по формуле:
D = b2 − 4ac.
Дискриминант для решения квадратных уравнений величина очень важная. Просчитав его, можно определить, сколько решений у уравнения, и есть ли они вообще. Вариантов всего три:
- D <, 0, корней нет,
- D = 0, есть один корень,
- D >, 0, корней два.
Формула дискриминанта и его корней универсальна и подходит для любого квадратного уравнения. Если решать задание последовательно, по определенному алгоритму, то найти корни несложно, даже в случае дробных коэффициентов.
Как пример использования формулы решим несколько простых уравнений:
x2 − 2x − 3 = 0.
Находим дискриминант:
D = (−2)2 − 4 · 1 · (−3) = 16, (a = 1, b = −2, c = −3).
Дискриминант положительный, значит, корней должно быть два. Записываем формулы и подставляем значения коэффициентов:
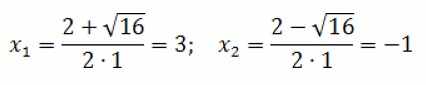
Уравнение 2:
15 − 2x − x2 = 0,
D = (−2)2 − 4 · (−1) · 15 = 64,
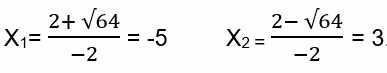
Уравнение 3:
4×2+21x+5=0.
Решение. a=4, b=21, c=5.
D=b2— 4ac=212— 4∙4∙5=441-80=361=192>,0, 2 действительных корня.
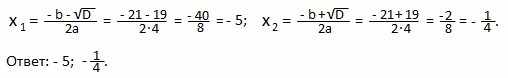
Чатов в заданиях ЕГЭ встречается вопрос: когда квадратное уравнение имеет бесконечное множество решений? В школьной программе эта тема проходит по касательной и многие ученики не успевают ее усвоить. Тем не менее, она очень важна. Потому что ответ такой: если это уравнение с параметрами. Это уравнения типа Уравнение вида Ах2+Вх+с = 0 где переменная, А, В и С не фиксированные коэффициенты, а параметры. То есть величины, которые могут принимать значения в определенном диапазоне числовой прямой.
Рассмотрим задачу: При каких значениях параметра a уравнение a(a+3)x2+(2a+6)x−3a−9 = 0 имеет более 1 корня?
Если a(a+3)=0, то уравнение превращается в линейное 6x−9=0 и имеет 1 корень, х=1,5.
При a≠0,a≠−3 получаем квадратное уравнение. Если
D>,0D>,0D/4= (a+3)2+3a(a+3)2>,0
D/4= (a+3)2+3a(a+3)2>,0
(a+3)2(3a+1)>,0
(a+3)2(3a+1)>,0
a>,−1/3.
Уравнение имеет два корня, если параметр находится в промежутке: a∈(−1/3,0)∪(0,+∞)
При a=−3 уравнение принимает вид 0=0, то есть корнями являются любые рациональные числа.
Полное решение уравнения выглядит так:
a∈−3∪(−13,0)∪(0,+∞).
Решение квадратных уравнений при помощи формулы корней – задача не сложная. Но есть и другие способы, например, графический. Но это предмет рассмотрения в другой статье.