Интегральное исчисление — сложная методика определения первичного вида функций (первообразной), обратная дифференцированию. Но, в отличие от дифференциала, найти интеграл сложнее. Если перед вами табличные интегралы, то можно воспользоваться готовыми формулами и решениями. Но так бывает не всегда. Например, для интегрирования сложных функций таблица не подходит. Вернее подходит, но в том случае, когда сложную функцию можно разложить определенным образом на составные части. Это только один из методов, который называется интегрирование по частям.
Часто использование методе приводит к появлению одного, или даже двух табличных функций. Именно для этого и используют метод. Чтобы использовать формулу, необходимо выучить таблицу интегралов, она не слишком объемна и вполне доступна для запоминания. Зачем учить? На экзамене или контрольной не всегда найдется учебник под рукой, или шпаргалка, где можно подсмотреть. В этом случае разложение интеграла по частям может оказаться бесполезным, вы просто остановитесь на полдороге.
Иногда у учеников и студентов возникает вопрос, что обозначает символ dx? Это наиболее элементарное понятие, которое нужно усвоить. Символ под знаком d показывает, какая из величин в выражении считается переменной для интегрирования. В случае dv интегрирование ведется по переменной v, даже если это функция, если du – то по u.
Метод интегрирования по частям в неопределенном интеграле используется в том случае, когда базовую подынтегральную функцию можно представить, как производную двух функций, u ∙v. Например, x sin x dx. Это произведение двух функций y=x и y= sin x. Именно на этом примере будем рассматривать, как происходит интегрирование по частям. Но сначала выведем формулу, которая используется для этого действия.
Для того чтобы понять суть выражения, необходимо вспомнить базовые правила интегрирования. Вспомним, что дифференциал произведения функций определяется по стандартной формуле:
1. d(uv) = udv + vdu.
Неопределённый интеграл от дифференциала некоторой функции равен самой функции:
2. d ( ∫ f (x) dx ) = f (x) dx.
Также припомним табличные интегралы для функций нашего примера:
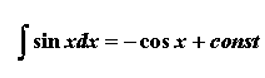
и
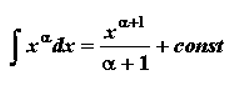
Допустим, что произведение uv — это дифференциал некой первообразной функции, которую нам предстоит найти. Воспользуемся выражениями 1 и 2 и проинтегрируем произведение наших функций:
uv = ∫ udv + ∫vdu, или, поменяв слагаемые местами, или:∫ udv = uv ∫vdu.
3. ∫ udv = uv ∫vdu.
Это и есть основная формула интегрирования по частям в неопределенном интеграле, которой мы будем пользоваться в дальнейшем.
Интегрирование — процесс творческий и не всегда строго регламентированный. В каждом сложном случае нужно искать свои пути решения. Но базовая формула всегда одна и та же. Рассмотрим, как проинтегрировать нашу функцию, которая приведена выше. Попробуем найти интеграл ∫ x sin x dx.
Распишем выражение, согласно формуле 3:
- ∫ x sin x dx = x cos x + ∫ cos x dx. Примем, что х, это u, а cos x — это v.
Внимательно посмотрев на запись, увидим, что выражение 3 полностью соответствует нашей записи под номером 4.
Но это только половина дела. Дальше интегрируем каждую часть выражения отдельно. Получаем:
x cos x = x cos x,
∫ cos x dx = sin x +С.
Результат запишем так — ∫ x sin x dx = -x cos x + sin x + C.
Просто? Если понять суть метода, правильно расписать сложную функцию в виде произведения более простых и уметь пользоваться таблицей интегралов, то задания на неопределенный интеграл не покажутся особенно сложными.
Таблица неопределённых интегралов.
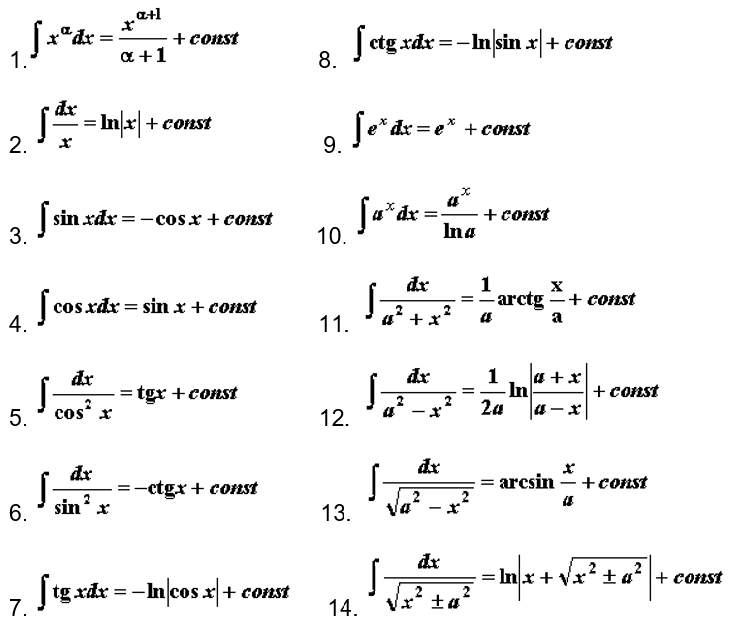
В каждом случае интегрирования по частям придется пользоваться данными этой таблицы. Лучше всего выучить ее и запомнить. Это сильно упростит работу по интегрированию.
Рассмотрим еще пример, более сложный, в котором интегрировать по частям нужно дважды:
Найти ∫x2cosxdx
Представим: u=x2 , dv=cosxdx, v=sinx, du=2xdx. Правильность хода решения во многом зависит от правильного выбора u и v.
Воспользуемся нашим выбором и запишем:
∫x2cosxdx = x2sinx−∫sinx⋅2xdx = x2sinx−2∫xsinxdx
Как видим, выражение не сильно упростились, одно из слагаемых все еще является интегралом произведения функций. Изменим обозначения:
u=x, du=dx, v=−cosx, dv=sinxdx
после подстановок и преобразований получим:
x2sinx−2(x⋅(−cos)x−∫(−cosx)dx) = x2sinx+2xcosx−2∫cosxdx = x2sinx+2xcosx−2sinx+C = (x2−1)sinx+2xcosx+C. Это и есть решение нашей задачи, то есть, первообразная функции x2cosx.
Метод довольно сложный для использования, но много задач не получится решить по- другому. Чтобы освоить его необходимо много практиковаться. Для начала берите самые простые примеры, постепенно усложняя задания. Так получится и освоить интегрирование по частям, и выучить таблицу более простых неопределенных интегралов.