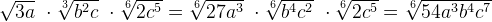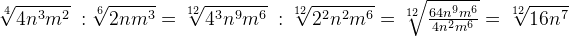Выражения, содержащие корень, который нельзя извлечь, называются иррациональными или радикальными.
Примеры:
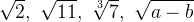иррациональные выражения.
Сложение и вычитание корней
При сложении или вычитании иррациональных выражений их пишут одно за другим с сохранением их знаков.
Примеры:
В некоторых случаях с помощью преобразования можно сделать иррациональные выражения подобными, то есть, имеющими одинаковые показатели корней и подкоренные числа (или выражения), а затем сделать приведение.
Примеры:
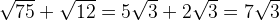
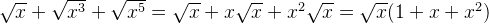
Умножение и деление корней
При умножении иррациональных выражений с одинаковыми показателями корней перемножаются их подкоренные числа или выражения:
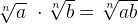
При делении иррациональных выражений с одинаковыми показателями корней подкоренное число или выражение делимого делится на подкоренное число или выражение делителя:
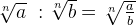
Примеры:
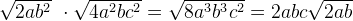
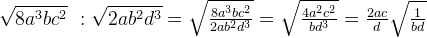
Возведение корня в степень
Чтобы возвести в степень иррациональное выражение, следует возвести в степень подкоренное число или выражение:
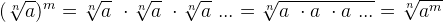
Примеры:
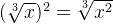
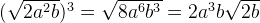
При возведении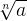 
в n-ю степень знак корня отбрасывается, так как возведение числа (или выражения) в n-ю степень и извлечение из него корня n-ой степени это взаимно сокращающиеся действия:
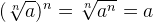
Извлечение корня
Чтобы извлечь корень из иррационального выражения, следует показатели корней перемножить:
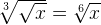, так как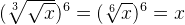 
Пример.
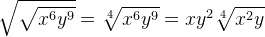
С помощью таких преобразований можно упростить извлечение корней 4-й, 6-й, 8-й, 9-й и т. п. степеней из чисел.
Примеры:
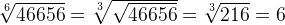
Сокращение корней
Величина иррационального выражения не изменится, если показатель корня и подкоренного выражения умножить или разделить на одно и то же число:
так как извлечение корня и возведение в степень это взаимно сокращающиеся действия, если их показатели равны.
На этом свойстве основано сокращение корней и приведение их к общему показателю.
Сокращение корней это деление показателей корня и подкоренного числа (или выражения) на одно и то же число, если оно является общим множителем для всех показателей.
Примеры:
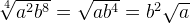
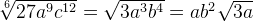
Приведение корней к общему показателю
Приведение корней к общему показателю имеет большое сходство с приведением дробей к общему знаменателю. Рассмотрим два способа:
- Показатели корней не имеют общих множителей. В этом случае показатель каждого корня и его подкоренное число (или выражение) умножают на произведение остальных корней.
Рассмотрим три выражения:
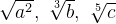,Так как у данных показателей нет общего множителя, то просто перемножаем все показатели между собой. Полученный результат и станет общим показателем. После приведения к общему показателю выражения будут иметь следующий вид:
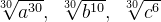
- Показатели корней имеют общий множитель. В этом случае надо найти НОК показателей и умножить показатель каждого корня на недостающий множитель.
Рассмотрим два выражения:
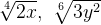,НОК (4, 6) = 12, значит, для первого выражения дополнительным множителем будет 3, а для второго 2. После приведения к общему показателю выражения будут иметь следующий вид:
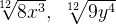
При умножении и делении иррациональных выражений с разными показателями их приводят к общему показателю, а затем уже умножают или делят их подкоренные числа или выражения.
Примеры:
