Величина это то, что можно измерить. Такие понятия, как длина, площадь, объём, масса, время, скорость и т. д. называют величинами. Величина является результатом измерения, она определяется числом, выраженным в определённых единицах. Единицы, в которых измеряется величина, называют единицами измерения.
Для обозначения величины пишут число, а рядом название единицы, в которой она измерялась. Например, 5 см, 10 кг, 12 км, 5 мин. Каждая величина имеет бесчисленное множество значений, например длина может быть равна: 1 см, 2 см, 3 см и т. д.
Одна и та же величина может быть выражена в разных единицах, например килограмм, грамм и тонна это единицы измерения веса. Одна и та же величина в разных единицах выражается разными числами. Например:
5 см = 50 мм (длина),
1 ч = 60 мин (время),
2 кг = 2000 г (вес).
Измерить величину значит узнать, сколько раз в ней содержится другая величина того же рода, принятая за единицу измерения.
Например, мы хотим узнать точную длину какой-нибудь комнаты. Значит нам нужно измерить эту длину при помощи другой длины, которая нам хорошо известна, например при помощи метра. Для этого откладываем метр по длине комнаты столько раз, сколько можно. Если он уложится по длине комнаты ровно 7 раз, то длина её равна 7 метрам.
В результате измерения величины получается или именованное число, например 12 метров, или несколько именованных чисел, например 5 метров 7 сантиметров, совокупность которых называется составным именованным числом.
Меры
В каждом государстве правительство установило определённые единицы измерения для различных величин. Точно рассчитанная единица измерения, принятая в качестве образца, называется эталоном или образцовой единицей. Сделаны образцовые единицы метра, килограмма, сантиметра и т. п., по которым изготавливают единицы для обиходного употребления. Единицы, вошедшие в употребление и утверждённые государством, называются мерами.
Меры называются однородными, если они служат для измерения величин одного рода. Так, грамм и килограмм меры однородные, так как они служат для измерения веса.
Единицы измерения
Ниже представлены единицы измерения различных величин, которые часто встречаются в задачах по математике:
Меры веса/массы:
- 1 тонна = 10 центнеров,
- 1 центнер = 100 килограмм,
- 1 килограмм = 1000 грамм,
- 1 грамм = 1000 миллиграмм.
Меры длины:
- 1 километр = 1000 метров,
- 1 метр = 10 дециметров,
- 1 дециметр = 10 сантиметров,
- 1 сантиметр = 10 миллиметров.
Меры площади (квадратные меры):
- 1 кв. километр = 100 гектарам,
- 1 гектар = 10000 кв. метрам,
- 1 кв. метр = 10000 кв. сантиметров,
- 1 кв. сантиметр = 100 кв. миллиметрам.
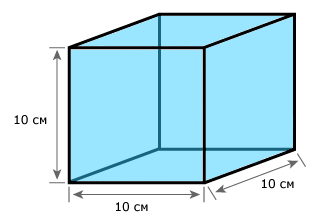
Меры объёма (кубические меры):
- 1 куб. метр = 1000 куб. дециметров,
- 1 куб. дециметр = 1000 куб. сантиметров,
- 1 куб. сантиметр = 1000 куб. миллиметров.
Рассмотрим ещё такую величину как литр. Для измерения вместимости сосудов употребляется литр. Литр является объёмом, который равен одному кубическому дециметру (1 литр = 1 куб. дециметру).
Меры времени:
- 1 век (столетие) = 100 годам,
- 1 год = 12 месяцам,
- 1 месяц = 30 суткам,
- 1 неделя = 7 суткам,
- 1 сутки = 24 часам,
- 1 час = 60 минутам,
- 1 минута = 60 секундам,
- 1 секунда = 1000 миллисекундам.
Кроме того, используют такие единицы измерения времени, как квартал и декада.
- квартал 3 месяца,
- декада 10 суток.
Месяц принимается за 30 дней, если не требуется определить число и название месяца. Январь, март, май, июль, август, октябрь и декабрь 31 день. Февраль в простом году 28 дней, февраль в високосном году 29 дней. Апрель, июнь, сентябрь, ноябрь 30 дней.
Год представляет собой (приблизительно) то время, в течении которого Земля совершает полный оборот вокруг Солнца. Принято считать каждые три последовательных года по 365 дней, а следующий за ними четвёртый в 366 дней. Год, содержащий в себе 366 дней, называется високосным, а годы, содержащие по 365 дней простыми. К четвёртому году добавляют один лишний день по следующей причине. Время обращения Земли вокруг Солнца содержит в себе не ровно 365 суток, а 365 суток и 6 часов (приблизительно). Таким образом, простой год короче истинного года на 6 часов, а 4 простых года короче 4 истинных годов на 24 часа, т. е. на одни сутки. Поэтому к каждому четвёртому году добавляют одни сутки (29 февраля).
Об остальных видах величин вы узнаете по мере дальнейшего изучения различных наук.
Сокращённые наименования мер
Сокращённые наименования мер принято записывать без точки:
Меры длины
| Меры веса/массы
|
Меры площади (квадратные меры)
| Меры объёма (кубические меры)
|
Меры времени
| Мера вместимости сосудов
|
 | 1 мм | 1 см | 1 дм | 1 м | 1 км |
 | 1 мм2 | 1 см2 | 1 дм2 | 1 м2 | 1 км2 |
 | 1 мм3 | 1 см3 | 1 дм3 | 1 м3 | 1 км3 |
Измерительные приборы
Для измерения различных величин используются специальные измерительные приборы. Одни из них очень просты и предназначены для простых измерений. К таким приборам можно отнести измерительную линейку, рулетку, измерительный цилиндр и др. Другие измерительные приборы более сложные. К таким приборам можно отнести секундомеры, термометры, электронные весы и др.
Измерительные приборы, как правило, имеют измерительную шкалу (или кратко шкалу). Это значит, что на приборе нанесены штриховые деления, и рядом с каждым штриховым делением написано соответствующее значение величины. Расстояние между двумя штрихами, возле которых написано значение величины, может быть дополнительно разделено ещё на несколько более малых делений, эти деления чаще всего не обозначены числами.
Определить, какому значению величины соответствует каждое самое малое деление, не трудно. Так, например, на рисунке ниже изображена измерительная линейка:

Цифрами 1, 2, 3, 4 и т. д. обозначены расстояния между штрихами, которые разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответствует 1 мм. Эта величина называется ценой деления шкалы измерительного прибора.
Перед тем как приступить к измерению величины, следует определить цену деления шкалы используемого прибора.
Для того чтобы определить цену деления, необходимо:
- Найти два ближайших штриха шкалы, возле которых написаны значения величины.
- Вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.

В качестве примера определим цену деления шкалы термометра, изображённого на рисунке слева.
Возьмём два штриха, около которых нанесены числовые значения измеряемой величины (температуры).
Например, штрихи с обозначениями 20 С и 30 С. Расстояние между этими штрихами разделено на 10 делений. Таким образом, цена каждого деления будет равна:
(30 С — 20 С) : 10 = 1 С
Следовательно, термометр показывает 47 С.
Измерять различные величины в повседневной жизни приходится постоянно каждому из нас. Например, чтобы прийти вовремя в школу или на работу, приходится измерять время, которое будет потрачено на дорогу. Метеорологи для предсказания погоды измеряют температуру, атмосферное давление, скорость ветра и т. д.