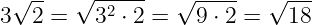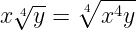Извлечь из данного числа корень какой-нибудь степени значит найти такое число, которое при возведении в эту степень, будет равно данному числу.
Из правил знаков при возведении в степень следует, что:
- Корень нечётной степени из положительного числа есть число положительное, а из отрицательного отрицательное.
Примеры:
3+27 = +3, так как (+3)3 = 27,
3-27 = -3, так как (-3)3 = -27.
- Корень чётной степени из положительного числа может быть как положительным, так и отрицательным числом.
Примеры:
+9 = ±,3, так как (+3)2 = +9 и (-3)2 = +9,
4+256 = ±,4, так как (+4)4 = +256 и (-4)4 = +256.
- Корень чётной степени из отрицательного числа является невозможным выражением, потому что любое положительное или отрицательное число при возведении в чётную степень даёт только положительный результат. Таким образом,
-49 , 4-256 , 6-64 это невозможные выражения.
Невозможные выражения иначе называют мнимыми.
Извлечение корня из произведения, степени и дроби
Чтобы извлечь корень из произведения, надо извлечь его из каждого множителя отдельно.
Так же можно сказать, что корень произведения равен произведению корней всех его множителей:
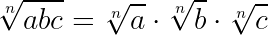
Чтобы извлечь корень из степени, следует показатель степени разделить на показатель корня:
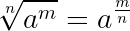
Чтобы извлечь корень из дроби, следует извлечь его отдельно из числителя и из знаменателя:
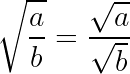
Примеры:
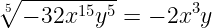
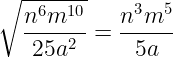
Вынесение множителя из-под знака корня
Когда нельзя извлечь корень из всего подкоренного числа или выражения, то подкоренное число или выражение раскладывают на множители и извлекают корень только из тех множителей, из которых это возможно сделать.
Примеры:
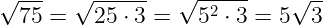
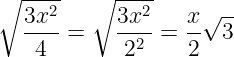
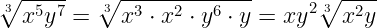
Внесение множителя под корень
Если нужно внести множитель под знак корня, то его следует возвести в степень, равную показателю корня.
Примеры: