Названия геометрических фигур происходят от количества их сторон. Например, треугольник, четырехугольник, пятиугольник. Но есть фигуры, которые названы по другим признакам, например, прямоугольник, квадрат, ромб, трапеция. Все эти фигуры — четырехугольники, но отличаются друг от друга величиной углов и сторон.
Прямоугольник — четырехугольник с разными сторонами у которого все углы по 90о.

Квадрат — прямоугольник, у которого все углы по 90 градусов и стороны равные.

Такие отличия есть и у других фигур, например, треугольники подразделяются на прямоугольные, равносторонние, равнобедренные и разносторонние. Свойства фигуры зависят как от количества сторон, так и от других характеристик — величины углов и сторон. Только измерив все параметры, можно точно описать фигуру и определить, какими формулами и правилами пользоваться при вычислениях.
Что такое геометрическая фигура
Под этим термином понимают часть плоскости, ограниченной несколькими замкнутыми (соединенными) линиями. В результате соединения линий образуется отрезки, которые называются сторонами фигуры и точки соприкосновения, которые носят название вершин. У треугольника три стороны и три вершины, у четырехугольника — четыре стороны и четыре вершины.
В геометрии есть фигуры, которые выпадают из этого ряда. Это точка, прямая линия, отрезок, луч. Отличаются они от остальных фигур, тем, что не занимают никакой площади, это просто части линии.
Что такое площадь
Теперь рассмотрим еще одно понятие геометрии — площадь. Это часть плоскости, которая находится внутри многоугольника. Другими словами, все, что находится между сторонами фигуры и является ее площадью. Геометрия — часть математики, то есть, наука точная, которая стремится все измерить и описать цифрами. Не стала исключением и площадь. Часть плоскости, которая находится внутри фигуры, разбили на маленькие части с равными сторонами, идущими под прямым углом друг к другу. Такая фигура называется квадрат.
Квадрат — геометрическая фигура из четырех равных сторон и четырех прямых углов.
За единицу площади взяли квадрат, сторона которого равна единице длины (1 миллиметр, 1 метр, 1 сантиметр). Площадь, которую занимает квадрат со стороной 1 сантиметр назвали квадратный сантиметр (обозначает см2). Если квадрат построен из сторон в 1 м, то его площадь 1 м2. Найти площадь фигуры — значит определить, сколько таких квадратиков можно поместить внутри фигуры.
Расчет площади прямоугольника
Разберем простую задачу — как высчитать площадь прямоугольника? Можно решить ее двумя способами. Самый простой, но самый длинный и трудоемкий — нарисовать прямоугольник и с помощью карандаша и линейки разбить его на маленькие квадратики. Затем посчитать количество квадратиков и узнать, сколько их поместилось внутри.
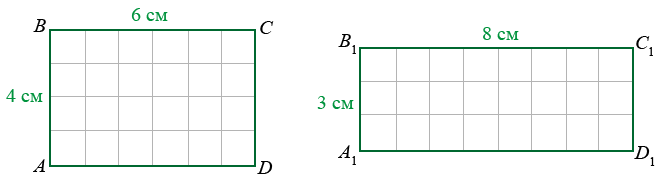
Такой способ простой и доступный, если длина сторон прямоугольника — целое количество сантиметров или метров. А вот при их нецелом количестве, например стороны три с половиной и четыре с половиной сантиметра (3,5 см и 4,5 см), посчитать сложнее. Еще сложнее, если стороны, например 3см и 2 мм и 4 см и 7 мм. Рисовать придется миллиметровые квадратики, что довольно сложно и долго.
Ученые древности, идя таким путем заметили интересную особенность, если посчитать квадраты внутри фигуры и сравнить их с результатом умножения длин сторон прямоугольника, то они окажутся одинаковыми. Проверив это на многих прямоугольниках и квадратах составили правило:
Площадь прямоугольника равна длине умноженной на ширину.

В учебниках можно найти и другую формулировку — площадь прямоугольника равна произведению соседних сторон, или еще иначе — площадь прямоугольника равна произведению основания на высоту. Суть этих утверждений одна и та же. Выражается она в формуле:
S=AB ∙BC.
Как уже говорилось, площадь измеряется в квадратных единицах — метрах, сантиметрах, дециметрах. Результат может быть как целым, так и дробным, например, 4 см2, 6 см2, или 4,6 см2 (4см2 и 6мм2).
Использование этой формулы — самый простой способ, как вычислить площадь прямоугольника с разными сторонами. Подходит он и для решения задачи вычисления квадрата (прямоугольника с равными сторонами). Для квадрата формула может выглядеть несколько иначе.
S=АВ2
Как она получалась? Начнем с основной формулы S=AB ∙BC. У квадрата АВ=ВС, отсюда S= АВ ∙ АВ = АВ2.
Периметр
Еще одна важная характеристика прямоугольника — периметр. Это сумма длин всех сторон. Периметр легко найти, измерив все стороны и сложив результаты. Но, как и в случае с площадью, лучше воспользоваться формулой. Сначала найдем периметр квадрата:
Р = АВ+ВС+СD+AD.
Но у квадрата все стороны одинаковые, значит, выражение можно записать иначе:
Р= АВ+АВ=АВ=АВ = 4 ∙ АВ, или 4АВ.
Для прямоугольника с разными сторонами периметр находится по такой же формуле:
Р = АВ+ВС+СD+AD.
Но здесь равны не все стороны, а только противоположные:
АВ= СD и ВС= AD
Перепишем начальную формулу по-другому:
Р= (АВ +СD) и (ВС + AD). Из равенства сторон получим Р=2АВ+2ВС + 2(АВ+ВС). Словами это будет звучать так:
Периметр прямоугольника равен сумме соседних сторон умноженной на два.
Как видно из приведенных утверждений, площадь и периметр прямоугольника можно вычислить двумя способами — непосредственным измерением и вычислением. Второй способ намного удобнее, особенно, если приходится находить площади и периметры реальных участков, например, площадки под строительство, дачного участка, комнаты.
Смотрите также другие геометрические фигуры: