Нет ничего полезнее в математике, чем умение высчитывать проценты. Это пригодится как в повседневной жизни, при планировании бюджета, например, или для проверки накопленной сумме на депозите, так и при написании контрольной работы или сдаче экзаменов, так что в экономической науке без процентов никуда. Процент — очень удобный способ счета в десятичной системе исчисления. Символ %, формула:
![]()
Правило говорит — процент, это сотая часть какого либо числа. Не обязательно сотни. Просто, чтобы найти один процент от конкретного числа, необходимо это число разделить на 100. Например, возьмём
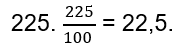
Часто удобнее пользоваться не обычной, а десятичной дробью. Напишем правило определения процента по- другому: один процент равен одной сотой части числа, записанный десятичной дробью, то есть 1% = 0,01. Соответственно 2% = 0,02, а 20% = 0,2.
Задача: Найти проценты от десятичной дроби 0,225. Для решения достаточно умножить десятичную дробь на 100, получим 0,225 x 100 =22,5%.
Перевод процентов в десятичные дроби — самый наглядный способ определения части числа. Например, у вас есть 1000 рублей и вам нужно купить вещь за 350 рублей. Сколько процентов бюджета придется истратить?.
Для решения такого типа задач составляем пропорцию:
1000 р – 100%
350р – х%.
Отсюда выплывает уравнение:
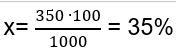
Далее переходим к десятичным дробям, 35 разделяем на 100 и получаем 0,35. Далее решаете сами, отдавать более трети наличных денег за покупку, или нет.
Для примера взяты круглые числа, которые легко делить у умножать. Но в реальной жизни цифры несколько другие. Существует более простая формула, как вычислить процентное соотношение двух чисел. Запомнив ее, достаточно легко решить задачу в уме, или при помощи калькулятора. Например, нужно найти, сколько процентов от числа X `составляет число Y. Используем формулу:
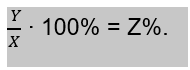
На конкретном примере это выглядит так: Найти, сколько процентов составляет число 34 от 135. Используем уже известную формулу:
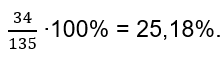
Обычно проценты закругляются до целых единиц, но есть случаи, когда важны даже тысячные доли процента, поэтому при решении задачи, как найти часть от целого в процентах нужно исходить из конкретной ситуации.
Задача обратная предыдущей. Опять перейдем в прикладную плоскость. Например, вам разрешено истратить не более 33% от выданной на руки суммы. Чтобы не упрощать вычисления, воспользуемся «неудобными» числами. У вас есть сумма в 1337 рублей, на какие деньги вы можете рассчитывать при поиске товара?
Можно опять составить пропорцию:
1337 р – 100%
Х 33%
В этом случае решение будет выглядеть так:
(1337 ∙ 33) : 100 = 44,21 р. Именно на такую сумму вы можете совершить покупку.
Готовая формула вычисления числа Х при известных процентах Z от числа Y выглядит так:
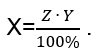
Правило формулируется так: умножаем процентное соотношение на большее число и делим на 100%. Формула простая и легко применимая в повседневной жизни.
Опять же начнем с прикладной задачи, так проще понять, зачем все это нужно. Задача простая, у одного ученика 230 друзей в социальной сети, а у другого — на 32% больше. Сколько друзей у другого ученика?
Сначала приведем абстрактную формулу:
А – известное число,
В – неизвестное число,
Р – разница в процентах.
Для вычисления числа В существует готовая формула, несколько громоздкая, но не сложная, если вдуматься:
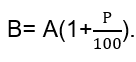
Для вычисления сначала производим деление, затем сложение в скобках и только потом умножение. Уточнение необходимо потому, что порядок действий — одна из самых распространенных ошибок учеников и многих студентов.
Воспользуемся формулой для решения нашей конкретной задачки:
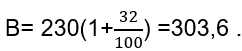
Получившееся дробное число не следует считать ошибкой — один из друзей находится в процессе регистрации.
Похожая формула используется, если одно число меньше другого на определенный процент. В этом случае выражение выглядит так:
В= А(1- Р/100).
Одна из самых полезных формул во время массового пользования кредитами и депозитами. Она позволяет найти, например, сколько вы получите через 3, 5 или 10 лет, если положили в банк деньги под определенные проценты. Также легко просчитать, как уменьшится стоимость вашей машины за 10 лет, если процент амортизации составляет 3% в год. Несложно будет и найти, сколько придется заплатить за новый телефон через 5 лет, если каждая модель выходит с периодичностью раз в год и дороже предыдущей на 30%.
Формула простая В= А(1+ Р/100)n.
Расшифруем ее:
В — сколько мы получим,
А — исходная цена (вклад),
Р — процентная ставка,
n — количество лет (месяцев, дней), то есть циклов по условиям договора.
Задачи, как высчитать процент о числа, найти число по процентам и более сложные нужно обязательно уметь решать, это основы экономической грамотности, которые всегда пригодятся в жизни. Не менее важно уметь работать с процентами для строителей, продавцов, инженеров и людей других специальностей.