Круг это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности радиусом круга:
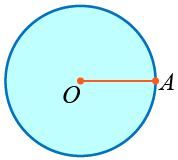
O центр круга, OA радиус круга.
Площадь круга
Площадь круга равна произведению числа на квадрат радиуса. Формула нахождения площади круга:
S = r2,
где S площадь круга, а r радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
| D = 2r, значит r = | D | . |
| 2 |
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = ( | D | )2 = | D2 | = | D2 | . |
| 2 | 22 | 4 |
Сектор круга. Площадь сектора
Сектор это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:
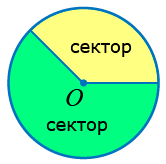
Чтобы найти площадь сектора, дуга которого содержит n, надо площадь круга разделить на 360 и полученный результат умножить на n.

Формула площади сектора:
| S = | r2 | ·, n = | r2n | , |
| 360 | 360 |
где S площадь сектора. Выражение
| r2n |
| 360 |
можно представить в виде произведения
| r2n | = n ·, | r | ·, | r | , |
| 360 | 180 | 2 |
| где | nr | это длина дуги сектора. |
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
| S = | sr | , |
| 2 |
где S это площадь сектора, s длина дуги данного сектора, r радиус круга.
Сегмент. Площадь сегмента
Сегмент это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:
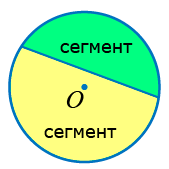
Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.

Площадь сегмента AMB будет вычисляться по формуле:
| S = | r | (s — BC), |
| 2 |
где S это площадь сегмента, r радиус круга, s длина дуги AB, а BC длина половины хорды двойной дуги.