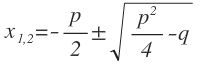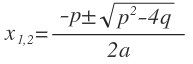Квадратное уравнение или уравнение второй степени с одним неизвестным это уравнение, которое после преобразований может быть приведено к следующему виду:
ax2 + bx + c = 0 квадратное уравнение,
где x это неизвестное, а a, b и c коэффициенты уравнения. В квадратных уравнениях a называется первым коэффициентом (a &ne, 0), b называется вторым коэффициентом, а c называется известным или свободным членом.
Уравнение:
ax2 + bx + c = 0
называется полным квадратным уравнением. Если один из коэффициентов b или c равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.
Приведённое квадратное уравнение
Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на a, то есть на первый коэффициент:
| x2 + | b | x + | c | = 0. |
| a | a |
Затем можно избавиться от дробных коэффициентов, обозначив их буквами p и q:
| если | b | = p, а | c | = q, |
| a | a |
то получится x2 + px + q = 0.
Уравнение x2 + px + q = 0 называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.
Например, уравнение:
x2 + 10x — 5 = 0
является приведённым, а уравнение:
-3×2 + 9x — 12 = 0
можно заменить приведённым уравнением, разделив все его члены на -3:
x2 — 3x + 4 = 0.
Решение квадратных уравнений
Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:
ax2 + bx + c = 0,
ax2 + 2kx + c = 0,
x2 + px + q = 0.
Для каждого вида уравнения есть своя формула нахождения корней:
| Вид уравнения | Формула корней | ||||
|---|---|---|---|---|---|
| ax2 + bx + c = 0 | 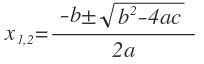 | ||||
| ax2 + 2kx + c = 0 | 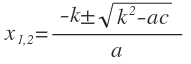 | ||||
| x2 + px + q = 0 |
|
Обратите внимание на уравнение:
ax2 + 2kx + c = 0
это преобразованное уравнение ax2 + bx + c = 0, в котором коэффициент b четный, что позволяет его заменить на вид 2k. Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё 2k вместо b:
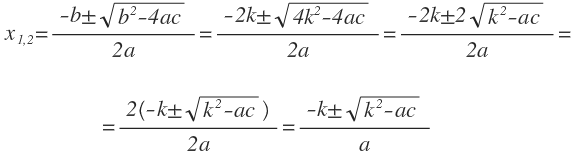
Пример 1. Решить уравнение:
3×2 + 7x + 2 = 0.
Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:
a = 3, b = 7, c = 2.
Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:
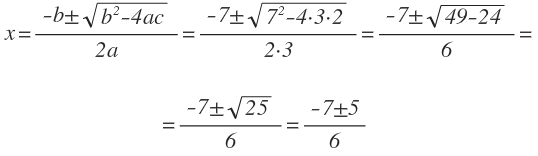
| x1 = | -2 | = — | 1 | , x2 = | -12 | = -2 |
| 6 | 3 | 6 |
| Ответ: — | 1 | , -2. |
| 3 |
Пример 2:
x2 — 4x — 60 = 0.
Определим, чему равны коэффициенты:
a = 1, b = -4, c = -60.
Так как в уравнении второй коэффициент чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:
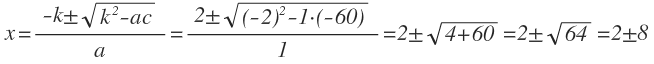
x1 = 2 + 8 = 10, x2 = 2 — 8 = -6
Ответ: 10, -6.
Пример 3.
y2 + 11y = y — 25.
Приведём уравнение к общему виду:
y2 + 11y = y — 25,
y2 + 11y — y + 25 = 0,
y2 + 10y + 25 = 0.
Определим, чему равны коэффициенты:
a = 1, p = 10, q = 25.
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:
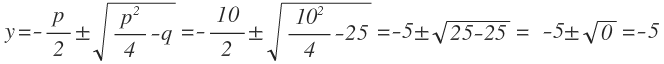
Ответ: -5.
Пример 4.
x2 — 7x + 6 = 0.
Определим, чему равны коэффициенты:
a = 1, p = -7, q = 6.
Так как первый коэффициент равен 1, то будем искать корни по формуле для приведённых уравнений с нечётным вторым коэффициентом:
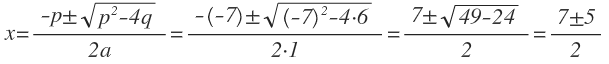
x1 = (7 + 5) : 2 = 6,
x2 = (7 — 5) : 2 = 1.
Ответ: 6, 1.