Логарифмы

Логарифм данного числа это показатель степени, в которую нужно возвести основание, чтобы получить данное число.

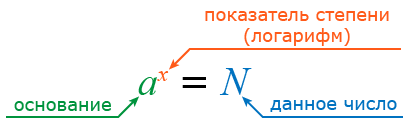
О равенстве ax = N можно сказать, что x это логарифм числа N по основанию a (где a &gt, 0 и a &ne, 1).

Слово логарифм сокращённо обозначается log, основание же, при котором указывается логарифм данного числа, обозначается в виде нижнего индекса с правой стороны log.

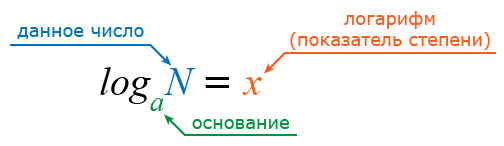
Если мы знаем, что логарифм числа N при основании a равен числу x, то есть:

logaN = x,

то это равенство можно написать без знака логарифма

ax = N,

где a основание степени, x показатель степени, N степень.

Оба равенства:

logaN = x и ax = N

выражают одну и ту же зависимость между числами a, x и N: если дано одно из равенств, значит можно написать и второе. Эту же зависимость между числами a, x и N можно выразить ещё одним равенством:

x N = a или a =x N .

Отрицательные числа и нуль ни при каком основании a (a &gt, 0 и a &ne, 1) логарифмов не имеют.

Основное логарифмическое тождество

Степень, показателем которой является логарифм числа N при таком же основании, как и основание степени, равна числу N.

alogaN = N.

Возьмём логарифм числа N при основании a равный числу q

logaN = q, значит aq = N.

Подставив в последнее равенство вместо числа q равное ему выражение logaN, получим

alogaN = N.

Выражение alogaN = N называется основным логарифмическим тождеством.

Свойства логарифмов

Рассмотрены свойства логарифмов для оснований, которые больше нуля и не равны единице:

a &gt, 0 и a &ne, 1.

Логарифм единицы равен нулю.

loga1 = 0,

так как нулевая степень любого числа (за исключением нуля) равна 1:

a0 = 1.

Логарифм числа равного основанию равен единице.

logaa = 1,

так как первая степень любого числа равна этому же числу без степени:

a1 = a.

Логарифм произведения равен сумме логарифмов сомножителей.

logaMN = logaM + logaN ,

где M &gt, 0, N &gt, 0.

Логарифм частного равен разности логарифмов делимого и делителя (или логарифм дроби равен логарифму числителя минус логарифм знаменателя).

loga	M	= logaM — logaN ,
	N

где M &gt, 0, N &gt, 0.

Логарифм степени равен произведению показателя степени на логарифм основания этой степени.

loga(N) = logaN ,

где N &gt, 0.

Логарифм, у которого в основании стоит степень, равен частному от деления логарифма при этом же основании без степени на показатель степени основания.

logaxN =	logaN	=	1	logaN ,
	x		x

где N &gt, 0, x &ne, 0.

Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня.

logax N =	logaN	=	1	logaN .
	x		x

Из формулы логарифма корня и формулы логарифма, у которого в основании стоит степень, можно сделать вывод, что логарифм корня равен логарифму данного числа с основанием в степени, равной показателю корня.

logax N = logaxN =	1	logaN .
	x

Свойства логарифмов степени и корня можно объединить ещё в одно:

logaN =		logaN ,

где N &gt, 0, &ne, 0.

Любой логарифм можно представить в виде отношения двух логарифмов, взятых по одному и тому же произвольному основанию.

logbN =	logaN	,
	logab

где N &gt, 0. Данная формула называется формулой перехода к новому основанию.

Произведение взаимно обратных логарифмов равно единице.

logba &middot, logab = 1.

Взаимно обратные логарифмы это пара логарифмов, у которых основание и выражение под знаком логарифма поменялись местами.

Величина логарифма не изменится, если возвести число, стоящее под знаком логарифма, и одновременно основание логарифма в какую-либо степень.

logaN = logaxNx,

где N &gt, 0, x &ne, 0.