Множество это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N множество натуральных чисел,
Z множество целых чисел.
Элемент множества это любой объект, входящий в состав множества. Принадлежность объекта к множеству обозначается с помощью знака . Запись
5Z
читается так: 5 принадлежит множеству Z или 5 элемент множества Z.
Множества делятся на конечные и бесконечные. Конечное множество множество, содержащее определённое (конечное) количество элементов. Бесконечное множество множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
L = {2, 4, 6, 8}
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
Подмножество
Подмножество это множество, все элементы которого, являются частью другого множества.
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
L = {2, 4, 6, 8} и M = {2, 4, 6, 8, 10, 12}.

Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком :
LM.
Запись LM читается так: множество L является подмножеством множества M.
Множества, состоящие из одних и тех же элементов, независимо от их порядка, называются равными и обозначаются знаком =.
Рассмотрим два множества:
L = {2, 4, 6} и M = {4, 6, 2}.
Так как оба множества состоят из одних и тех же элементов, то L = M.
Пересечение и объединение множеств
Пересечение двух множеств это совокупность элементов, принадлежащих каждому из этих множеств, то есть их общая часть. Пересечение обозначается знаком .
Например, если
L = {1, 3, 7, 11} и M = {3, 11, 17, 19}, то LM = {3, 11}.
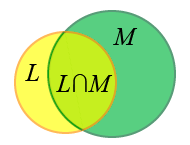
Запись LM читается так: пересечение множеств L и M.
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.
Объединением двух множеств называется множество, содержащее все элементы исходных множеств в единственном экземпляре, то есть если один и тот же элемент встречается в обоих множествах, то в новое множество этот элемент будет включён только один раз. Объединение обозначается знаком .
Например, если
L = {1, 3, 7, 11} и M = {3, 11, 17, 19},
то LM = {1, 3, 7, 11, 17, 19}.
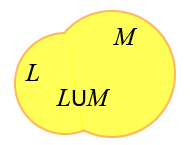
Запись LM читается так: объединение множеств L и M.
При объединении равных множеств объединение будет равно любому из данных множеств:
если L = M, то LM = L и LM = M.