Неравенства с одной переменной

Линейное неравенство с одной переменной это неравенство, которое можно привести к виду:

ax &gt, b или ax &lt, b.

Где x это переменная, a коэффициент, а b свободный член.

Если a &gt, 0, то, разделив обе части неравенства на a, получим:

x &gt,	b	или x &lt,	b	.
	a		a

Данные неравенства и определяют все значения переменной x, при которых данное неравенство будет верным. Оба неравенства можно изобразить с помощью числовых промежутков:

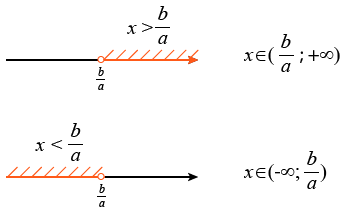
Обратите внимание, что в строгих неравенствах значение, с которым сравнивается переменная, не входит в множество значений самой переменной. В нестрогих неравенствах оно будет входить в множество допустимых значений:

если x	b	, то x [	b	, +)
	a		a

или

если x	b	, то x (-,	b	]	.
	a		a

Если a &lt, 0, то, разделив обе части неравенства

ax &gt, b или ax &lt, b

на a и поменяв в них знак на противоположный, получим:

x &lt,	b	или x &gt,	b	.
	a		a

Все возможные значения данных неравенств мы уже рассмотрели выше.

Если a = 0, тогда неравенство примет вид:

0 &middot, x &gt, b или 0 &middot, x &lt, b.

В первом случае:

0 &middot, x &gt, b, x (-, +),

если b отрицательное число, в противном случае неравенство не имеет решений.

Во втором случае:

0 &middot, x &lt, b, x (-, +),

если b положительное число, в противном случае неравенство не имеет решений.

Равносильные неравенства

Равносильные неравенства это неравенства, у которых совпадает множество решений. Неравенства, не имеющие решений, тоже считаются равносильными.

Неравенство, равносильное данному, получится, если:

1. Перенести слагаемое из одной части неравенства в другую, изменив знак слагаемого на противоположный.
2. Умножить или разделить обе части неравенства на одно и то же положительное число.
3. Умножить или разделить обе части неравенства на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.

Решение неравенств

Решить неравенство с одной переменной это значит, найти все значения этой переменной, при которых данное неравенство верно, или убедиться, что таких значений у переменной нет.

Все неравенства с одной переменной решаются одинаково с помощью преобразований, которые могут выполняться в любом порядке. Список возможных преобразований, которые могут быть использованы для решения неравенств:

• освобождение от дробных членов,
• раскрытие скобок,
• перенос всех членов, содержащих переменную, в одну часть, а остальных в другую (члены с переменными, как правило, переносят в левую часть неравенства),
• приведение подобных членов,
• деление обеих частей неравенства на коэффициент при переменной.

Пример 1. Решить неравенство и изобразить множество решений на координатной прямой:

-8x — 2 &gt, 14.

Решение: Переносим -2 в правую часть:

-8x &gt, 14 + 2

-8x &gt, 16

Делим обе части неравенства на -8:

-8x : (-8) &lt, 16 : (-8)

x &lt, -2

Отмечаем множество значений x на координатной прямой:

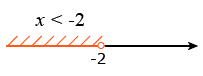
Ответ: (-, -2).

Пример 2. Решить неравенство и изобразить множество решений на координатной прямой:

6(y + 12) 3(y — 4).

Решение: Сначала раскрываем скобки:

6y + 72 3y — 12

Переносим 72 в правую часть, а 3y в левую и делаем приведение подобных слагаемых:

6y — 3y -12 — 72

3y -84

Делим обе части неравенства на коэффициент при неизвестном (на 3):

(3y) : 3 (- 84) : 3

y -28

Отмечаем множество значений y на координатной прямой:

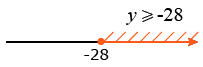
Ответ: [-28, +).