Одночлен это алгебраическое выражение, представляющее собой число, переменную, их степени с натуральным показателем, а также любые произведения, составленные из них.
Пример. 12, , m, (-2)3, a2, 5abc, a3x, 3,7c(-2ab2) одночлены.
Выражения x + 2 или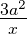 
не являются одночленами, так как представляют сумму или частное переменных и числа.
Число 0 называют нулевым одночленом.
Буквы и числа одночлена, представляющего собой произведение, называют множителями данного одночлена. При этом числа называют числовыми множителями одночлена, а буквы буквенными множителями одночлена.
Пример. Назовите числовые и буквенные множители одночлена 5abc.
Решение:
Множителями данного одночлена являются число 5 и буквы a, b, c:
Числовой множитель: 5.
Буквенные множители: a, b, c.
Стандартный вид одночлена
Стандартный вид одночлена это запись одночлена, представляющая собой число, степень переменной или произведение, в котором только один числовой множитель, записанный на первом месте, а каждая его буква участвует в его записи лишь один раз, при этом буквы записаны в алфавитном порядке.
Пример. 7, a, -3xy2, 1abс одночлены стандартного вида.
А вот следующие одночлены записаны не в стандартном виде:
12aa3b и 4cb(−2)y,
так как первый содержит одинаковые буквы, а во втором два числовых множителя и буквенные множители записаны не в алфавитном порядке.
Стандартный вид нулевого одночлена есть 0.
Коэффициент одночлена
Коэффициент одночлена это числовой множитель в одночлене стандартного вида, который содержит хотя бы одну переменную. Понятие коэффициент также относят к одночленам стандартного вида, представляющим собой числа без буквенных множителей. Коэффициентами таких одночленов считаются сами числа.
Пример. Одночлены
-7ab3, 
, -1x, 15
записаны в стандартном виде. Их коэффициенты соответственно равны числам -7, , -1, 15.
Коэффициент одночлена, равный 1 или -1 обычно не пишут.
Если одночлен имеет только буквенные множители, то условились считать, что его коэффициент равен +1 или -1, в зависимости от знака, который стоит (или подразумевается) перед одночленом.
Пример. Одночлены
a, -xy
записаны в стандартном виде. Коэффициент первого из них равен 1, второго -1, так как
a = 1 ·, a, -xy = -1 ·, xy.
Целый положительный коэффициент означает, сколько раз повторяется слагаемым буквенное выражение, перед которым он стоит.
Пример.
3ab = (ab) ·, 3 = ab + ab + ab.
Дробный положительный коэффициент означает, какая часть берётся от буквенного выражения, к которому он относится.
Пример. В одночлене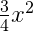 
коэффициент означает, что от x2 берётся , потому что 
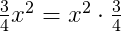, а умножить на значит взять от множимого.
Отрицательный коэффициент означает, что буквенное выражение, перед которым он стоит, умножается на абсолютную величину этого коэффициента и результат берётся с противоположным знаком.
Пример.
-4mn = -4 ·, mn = -(mn + mn + mn + mn).
Приведение одночлена к стандартному виду
С одночленами удобнее работать, когда они записаны в стандартном виде. Любой одночлен можно привести к стандартному виду путём тождественных преобразований. Процесс таких преобразований называют приведением одночлена к стандартному виду.
Привести одночлен к стандартному виду значит выполнить с ним такие тождественные преобразования, чтобы он принял стандартный вид.
Чтобы привести одночлен к стандартному виду надо:
- Выполнить группировку числовых множителей (если их несколько), а также одинаковых буквенных множителей и их степеней.
- Вычислить произведение числовых множителей и по свойству степеней с одинаковыми основаниями перемножить буквенные множители.
- Поставить на первое место числовой множитель, а после него расположить буквенные множители в алфавитном порядке.
Пример 1. Запишите одночлен -2b(-3)x34ab2x2 в стандартном виде.
Решение:
Используя переместительное и сочетательное свойства умножения, сгруппируем по отдельности числовые и одинаковые буквенные множители. В результате исходный одночлен примет вид:
((-2) ·, (-3) ·, 4) ·, (b ·, b2) ·, (x3 ·, x2) ·, a.
Перемножаем числовые множители и степени с одинаковыми основаниями. Произведение числовых множителей равно 24. Произведение степеней b равно b ·, b2 = b3. Произведение степеней x равно x3 ·, x2 = x5:
24 ·, b3 ·, x5 ·, a.
Записываем на первом месте числовой множитель, а после него располагаем буквенные множители в алфавитном порядке. В итоге получаем одночлен стандартного вида:
24ab3x5.
Следовательно:
-2b(-3)x34ab2x2 = ((-2) ·, (-3) ·, 4) ·, (b ·, b2) ·, (x3 ·, x2) ·, a = 24 ·, b3 ·, x5 ·, a = 24ab3x5.
Пример 2. Представить одночлен -2a4c0b в стандартном виде.
Решение:
Среди своих множителей, данный одночлен имеет множитель 0, значит всё произведение в результате будет равно 0. Стандартный вид нулевого одночлена есть 0:
-2a4c0b = 0.