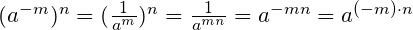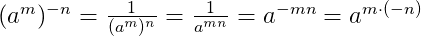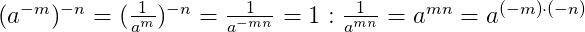Степень с отрицательным показателем
Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем.
| d -c = | 1 | , 7 -5 = | 1 | , a -5 = | 1 | . |
| d c | 7 5 | a 5 |
Чтобы разобраться, почему число в отрицательной степени равно дроби, надо вспомнить правило деления степеней с одинаковыми основаниями:
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
a 5 : a 8 = a5 — 8 = a -3.
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
| a 5 | = | 1 | . |
| a 8 | a 3 |
Значит:
| a -3 = | 1 | . |
| a 3 |
Пример 1. Замените дробь степенью с отрицательным показателем:
| 1 | . |
| x 2 |
Решение:
| 1 | = x -2. |
| x 2 |
Пример 2. Представьте в виде степени с отрицательным показателем:
| 1 | . |
| (m + n) 2 |
Решение:
| 1 | = (m + n) -2. |
| (m + n) 2 |
Действия над степенями с отрицательными показателями
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:
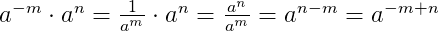
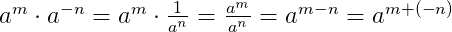
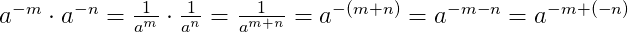
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:
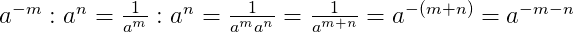
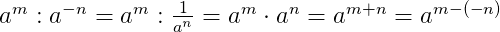
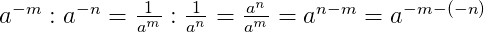
Чтобы возвести произведение в отрицательную степень, надо возвести в эту степень каждый сомножитель отдельно:
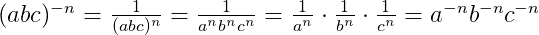
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
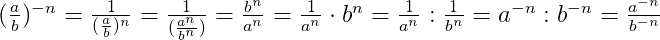
При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются: