Параллелограмм это четырёхугольник, у которого противоположные стороны параллельны. Если у параллелограмма все углы прямые, то такой параллелограмм называется прямоугольником, а прямоугольник, у которого все стороны равны, называется квадратом.
Все параллелограммы обладают следующими свойствами:
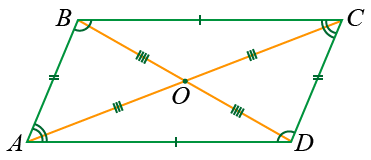
- противоположные стороны равны:
AB = CD и BC = DA,
- противолежащие углы равны:
ABC = CDA и DAB = BCD,
- сумма углов, прилежащих к одной стороне, равна 180:
ABC + BCD = 180,
BCD + CDA = 180,
CDA + DAB = 180,
DAB + ABC = 180,
- в точке пересечения диагонали делятся пополам:
AO = OC и BO = OD,
- каждая диагональ делит параллелограмм на два равных треугольника:
ABC = CDA и ABD = BCD,
- точка пересечения диагоналей это центр симметрии параллелограмма:
Точка O это центр симметрии.
Высота
Нижняя сторона параллелограмма называется его основанием, а перпендикуляр, опущенный на основание из любой точки противоположной стороны, высотой.
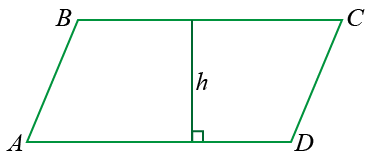
AD это основание параллелограмма, h высота.
Высота выражает расстояние между противоположными сторонами, поэтому определение высоты можно сформулировать ещё так: высота параллелограмма это перпендикуляр, опущенный из любой точки одной стороны на противоположную ей сторону.
Площадь
Для измерения площади параллелограмма можно представить его в виде прямоугольника. Рассмотрим параллелограмм ABCD:

Построенные высоты BE и CF образуют прямоугольник EBCF и два треугольника: ABE и DCF. Параллелограмм ABCD состоит из четырёхугольника EBCD и треугольника ABE, прямоугольник EBCF состоит из того же четырёхугольника и треугольника DCF. Треугольники ABE и DCF равны (по четвёртому признаку равенства прямоугольных треугольников), значит и площади прямоугольника с параллелограммом равны, так как они составлены из равных частей.
Итак, параллелограмм можно представить в виде прямоугольника, имеющего такое же основание и высоту. А так как для нахождения площади прямоугольника перемножаются длины основания и высоты, значит и для нахождения площади параллелограмма нужно поступить также:
площадь ABCD = AD ·, BE.
Из данного примера можно сделать вывод, что площадь параллелограмма равна произведению его основания на высоту.
Общая формула площади параллелограмма:
S = ah,
где S это площадь параллелограмма, a основание, h высота.