Подобные треугольники это треугольники, у которых все три угла равны, а все стороны одного треугольника в одно и то же число раз длиннее (или короче) сторон другого треугольника, то есть треугольники подобны если их углы равны, а сходственные стороны пропорциональны.
Сходственные стороны это стороны двух треугольников, лежащие против равных углов.
Рассмотрим два треугольника 
ABC и A1B1C1, у которых A = A1, B = B1, C = C1:
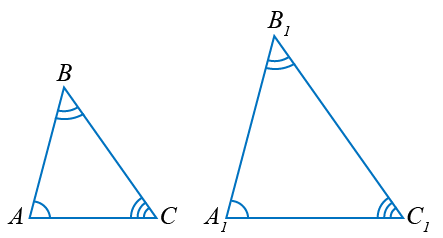
Стороны AB и A1B1, BC и B1C1, CA и C1A1, лежащие напротив равных углов, называются сходственными сторонами. Следовательно, отношения сходственных сторон равны:
| AB | = | BC | = | AC | = k, |
| A1B1 | B1C1 | A1C1 |
k это коэффициент подобия ( число, равное отношению сходственных сторон подобных треугольников). Если k = 1, то треугольники равны, то есть равенство треугольников это частный случай подобия.
Подобие треугольников обозначается знаком ~: ABC ~ A1B1C1.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если обозначить площади двух подобных треугольников буквами S и S1, то:
| S | = k2. |
| S1 |
Первый признак подобия треугольников
Если два угла одного треугольника равны двум углам другого, то треугольники подобны.
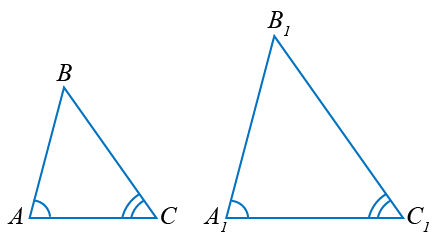
Если A = A1, C = C1,
то ABC ~ A1B1C1.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.
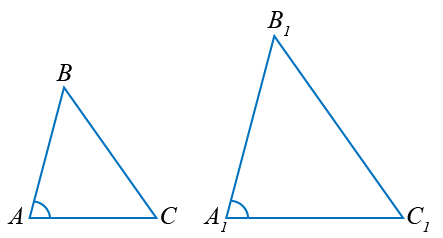
| Если | AB | = | AC | , A = A1, |
| A1B1 | A1C1 | |||
| то ABC ~ A1B1C1. | ||||
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.
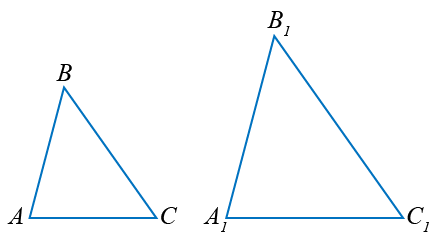
| Если | AB | = | BC | = | AC | , |
| A1B1 | B1C1 | A1C1 | ||||
| то ABC ~ A1B1C1. | ||||||