Название производной происходит от слова «произведенная», то есть образованная от другой величины. Производная функции характеризует темп изменения функции.
Процесс определения производной какой-либо функции называется дифференцированием. Если говорить совсем просто, то для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию.
Определение производной
Производная измеряет крутизну графика функции в определенной точке графика. Таким образом, производная это наклон. Это означает, что это отношение изменения значения функции к изменению независимой переменной.
Если независимой переменной оказывается время, мы часто думаем об этом соотношении как о скорости изменения.
Если мы увеличим масштаб графика функции в некоторой точке так, чтобы функция выглядела почти как прямая линия, производная в этой точке это наклон линии. Это то же самое, что сказать, что производная это наклон касательной к графику функции в данной точке.
Наклон секущей линии (линия, соединяющая две точки на графике) приближается к производной, когда интервал между точками уменьшается до нуля.
Производная также является функцией: она меняется от места к месту. Например, скорость автомобиля может меняться от момента к моменту, когда водитель ускоряется или замедляется.
Последнее замечание очень важное и интересное: оно говорит нам о том, что когда мы закончили определять производную какой-то конкретной функции везде, мы получаем другую функцию! Тогда мы могли бы поговорить о его производной! Конечно, мы делаем это очень часто, не осознавая этого! Всякий раз, когда мы говорим об ускорении, мы говорим о производной, то есть о скорости изменения скорости. Вторые производные (и третьи производные и т. д.)
Мы использовали много слов, чтобы попытаться описать производную. Математики стараются избегать большого количества слов, стремясь к точности и лаконичности. Давайте посмотрим, что они могут сделать вместо этого.
ФОРМУЛЫ НАХОЖДЕНИЯ ПРОИЗВОДНЫХ ОСНОВНЫХ ФУНКЦИЙ
Некоторые функции уже имеют известную производную. Кстати, производная функции тоже функция.
ЧИСЛО, СТЕПЕННАЯ ФУНКЦИЯ, ФУНКЦИЯ С КОЭФФИЦИЕНТОМ
В таблице приведены формулы для определения производной степенной функции и функции, заданной числом. 
ПРОИЗВОДНАЯ ОТ ПОКАЗАТЕЛЬНО-СТЕПЕННОЙ И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ
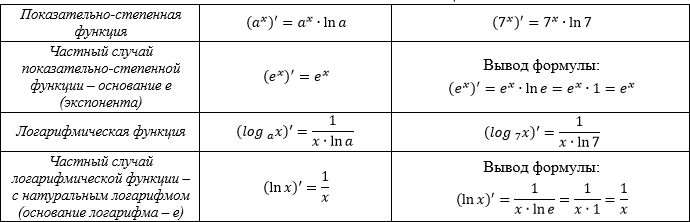
ПРОИЗВОДНАЯ ОТ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ


ПРОИЗВОДНАЯ ОТ ОБРАТНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
