При изучении геометрии вы непременно обращали внимание, что часть фигур очень похожа на другие. Отличаются только размеры. Но геометрия — наука точная и слово «похожие» не всегда определяет реальное положение вещей. Например, прямоугольный треугольник похож на равносторонний, но при ближайшем рассмотрении легко обнаружить различия, — отличаются углы, длины сторон, конфигурация.
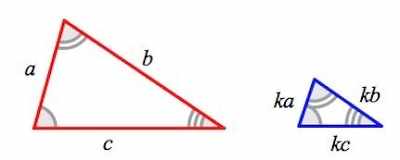
В геометрии применяется другое понятие — «подобие». Это более узкий термин, который определяет фигуры, которые идентичны по всем параметрам, кроме размера. Если увеличить, или уменьшить одну из фигур, то получится другая, с полным соответствием. Знак подобия в геометрии ~ имеет очень большой смысл. Это не просто обозначение «похожести», а специальный термин. Он говорит о том, что из одной фигуры можно получить другую, если преобразовать ее особым образом.
Самый простой способ — увеличение размеров. Но не простое увеличение, а пропорциональное. То есть, каждая сторона фигуры увеличивается на строго определенную величину. Соотношение новой длины и исходной называется коэффициентом подобия. Согласно правилам математики К≠ 0. Смысл ясен, на ноль делить нельзя. В остальном значение К может принимать любое значение, в том числе, и дробное. Если в десятичном исчислении коэффициент находится в диапазоне от ноля до единицы, то фигура уменьшается при проецировании, если К ≥ 1, то фигура получится больше, или идентичной исходной.
Каждая из геометрических фигур имеет ряд признаков, по которым ее можно сравнить с другой и определить, подобные фигуры, или просто похожие. У треугольников таких признаков три. Рассмотрим их более подробно. В идеале, треугольники называются подобными, если у них три угла одинаковые, а три стороны пропорциональны, согласно коэффициенту К. Но не всегда есть возможность измерить углы и стороны. Есть ряд признаков, требующих меньшего числа измерений, по которым легко определить, подобные треугольники, или нет.
Первый признак подобия
Если два угла произвольного треугольника равны двум углам другого, значит, фигуры подобные. В геометрической графике это записывается так:
ΔАВС ~ΔА1В1С1 А=∠А1, ∠В=∠В1, ∠С=∠С1.
Доказательство первого признака подобия приводить не будем, ввиду того, что признак проверен и доказан, информация об этом есть в любом учебнике. Намного важнее, что из этого признака вытекает следствие, которое не менее важно, чем сам признак. Во многих задачах на ЕГЭ и в учебниках упор делается именно на знание этого правила. «Если три стороны одного треугольника попарно параллельны трем сторонам другого, то эти фигуры подобны».
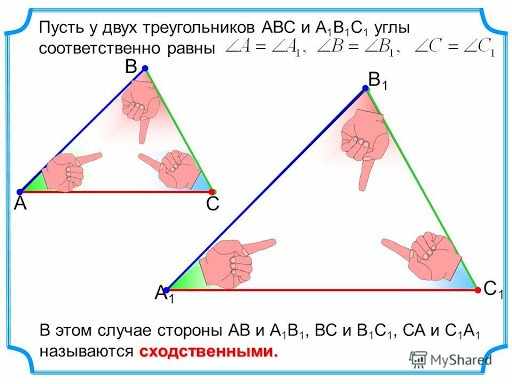
Утверждение не менее очевидно, чем первый признак подобия. Формулируется оно так:
Если две соответствующие стороны треугольников пропорциональны, а углы между ними равные, то фигуры подобные.
Это правило называется признаком подобия по двум сторонам и углу между ними. Геометрическая запись выглядит так:
ΔАВС ~ΔА1В1С1 ↔, ∠ А=∠А1, АВ/А1В1 = АС/А1С1.
Самый простой и наиболее понятный признак подобия: если три стороны одной фигуры пропорциональны трем сторонам другой с одинаковым коэффициентом К, то треугольники подобные. Записывается такое утверждение таким образом:
ΔАВС ~ΔА1В1С1↔,АВ/А1В1 = АС/А1С1= ВС/В1С1..
Доказательство этого утверждения опять же приводить не будем вследствие дефицита размера статьи. Лучше остановимся на следствиях, которые вытекают из этих утверждений. Многие из параметров геометрических фигур можно определить, пользуясь названными правилами.
Один из способов применения признаков подобия демонстрирует теорема об отношении периметров подобных треугольников. В формулировке говорится о том, что отношение периметров подобных треугольников равно коэффициенту пропорциональности сторон. На практике это выглядит так — вам нужно найти периметр треугольника со сторонами в несколько километров, что часто требуется в строительстве, агротехнике и геодезии. Если нарисовать подобный треугольник на бумаге, со сторонами в несколько сантиметров и вычислить периметр, то он будет ровно настолько же меньше, как и стороны треугольников. То есть, коэффициент К работает и в случае с периметром.
Вторая задача — найти соотношение площадей подобных треугольников. Здесь тоже существует определенная пропорция, но уже квадратичная. То есть, соотношение площадей фигур равно квадрату К.
S1/S = k2.
При решении задач поможет также лемма о подобных треугольниках, говорящая о том, что любая прямая, пересекающая треугольник параллельно одной из сторон, отсекает от него подобную фигуру.
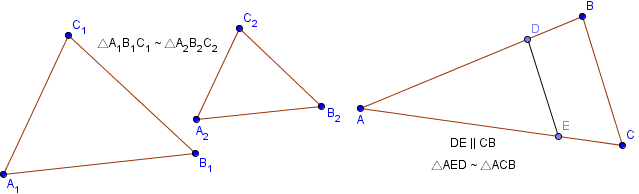
Пользуясь полученной информацией, несложно решить любую задачу по определению параметров подобных треугольников.