Движением тела называется изменение его положения в пространстве относительно других. Рассмотрим равномерное прямолинейное движение тела, для этого введем следующие понятия.
Определение равномерного прямолинейного движения тела
Равномерное прямолинейное движение тела это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Координата— величина, служащая для определения положения какой-либо точки на плоскости или в пространстве.
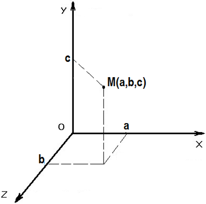
Перемещением тела называется вектор, соединяющий начальное положение тела с его последующим положением.
Траектория — это линия, вдоль которой движется тело.
Путь — это длина траектории, вдоль которой движется тело.

Скоростью равномерного прямолинейного движения называется величина, равная отношению перемещения тела к времени t, за которое это перемещение произошло .
Скорость ― это векторная величина!
В заданиях, где дана зависимость скорости тела от времени,
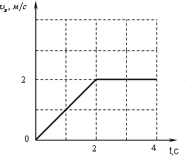
пройденный путь можно вычислить как площадь под графиком:
Следующие три переменные включены в равномерное прямолинейное движение:
Координаты: координата, с которой тело начинает двигаться (начальная позиция) и координата, куда он прибывает через некоторое время (конечная позиция) и координата, куда он прибывает через некоторое время (конечная позиция) . Скорость: скорость всегда будет постоянной . Время: момент, в который объект начинает двигаться (начальное время) и время, необходимое для прохождения определенного расстояния (конечное время) и время, необходимое для прохождения определенного расстояния (конечное время) . Эти три переменные связаны этой формулой:
,
где .
Равноускоренное прямолинейное движение
Равноускоренное прямолинейное движение тела движение, при котором его ускорение не меняется, ни по величине, ни по направлению.
Уравнение равноускоренного движения в проекции на ось Ox имеет вид:
, где:
начальная координата тела,
проекция начальная скорость на ось x,
проекция ускорения на ось x,
время движения
Ускорением тела называется векторная величина, равная отношению изменения скорости за любой промежуток времени к величине этого промежутка:
Зависимость скорости от времени при наличии ускорения определяется выражением:
, где:
скорость тела в момент времени t, t время,
начальная скорость тела, ускорение тела.
Применение производной в кинематике
Если существует зависимость координаты от времени x(t), то зависимость скорости от времени можно получить, взяв производную по времени от этой зависимости.
Скорость ― это производная координаты тела по времени:
Например, если зависимость координаты тела при равноускоренном движении имеет вид , то взяв первую производную от координаты, мы получим зависимость скорости тела от времени:
Точно также, ускорение ― это производная от скорости тела:
.
Примеры выполнения заданий ЕГЭ по физике
Задание 1.
На рисунке представлен график зависимости пути S, пройденного материальной точкой, от времени t. Определите, сколько секунд, после начала движения, когда точка стала двигаться со скоростью 10 м/с.
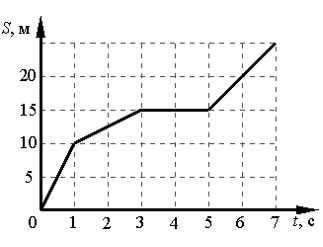
Ответ:1
Решение: Чтобы определить скорость движения точки на интервале, разделим путь, пройденный точкой, на все время движения на каждом отрезке графика. На интервале с начала движения и до 1 с точка прошла 10 м, следовательно, ее скорость была 10 м/с. Скорость точки на следующих интервалах пути ― 2,5 м/с, 0 м/с и 5 м/с соответственно.
Задание 2.
На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке х= 0, а пункт Б ― в точке х= 30 км. Чему равна скорость автобуса на пути из А в Б? Ответ выразить в км/ч.
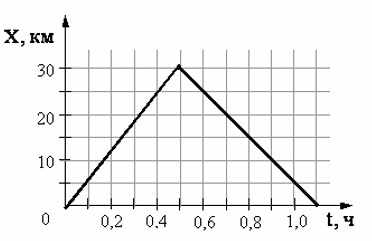
Ответ: 60 км/ч
Решение:
Согласно графику, зависимость пути автобуса от времени линейна, следовательно, скорость автобуса на всех участках пути постоянна. Из пункта А в пункт Б, находящиеся друг от друга на расстоянии S = 30 км автобус идет
t = 0,5 ч.
Уравнение движения автобуса: S = vt, откуда v = S/t = 30 км/ 0,5 ч = 60 км/ч.
Задание 3.
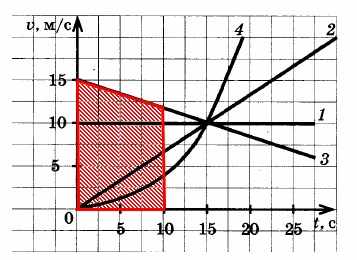
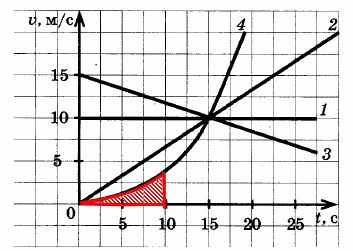
На рисунке изображены графики зависимости модуля скорости движения четырех автомобилей от времени. Какой из автомобилей — 1, 2, 3 или 4 — прошел наибольший путь за первые 10 с движения?
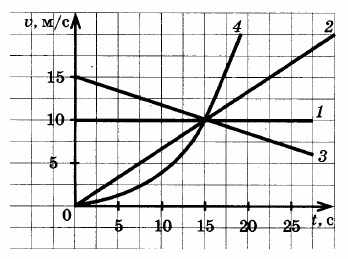
Ответ: 3
Решение:
Путь, пройденный каждым из автомобилей, равен площади под соответствующим графиком зависимости модуля скорости автомобиля от времени движения.
Как видно из следующих рисунков, наименьшая площадь под графиком скорости автомобиля 4, наибольшая ― под графиком скорости автомобиля 3.
Автомобиль 1 прошел путь:
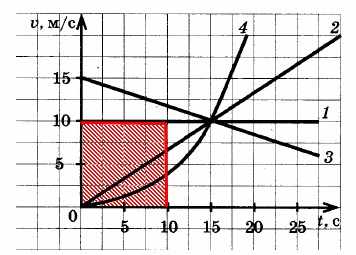
Автомобиль 2 прошел путь:
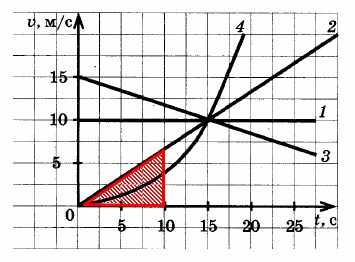
Автомобиль 3:
Путь, который проехал автомобиль 4:
Задание 4.
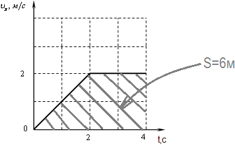
На рисунке представлен график зависимости скорости v автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 3 с.
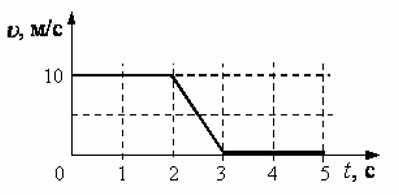
Ответ: 25 м
Решение: Путь, пройденный автомобилем, равен площади под соответствующим графиком зависимости модуля скорости автомобиля от времени движения.
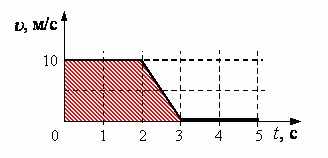
Площадь образовавшейся трапеции равна: м.
Задание 5.
Тело движется по оси x. По графику зависимости проекции скорости тела υx от времени t установите, какой путь прошло тело за время от t1= 0 до t2= 4 c.
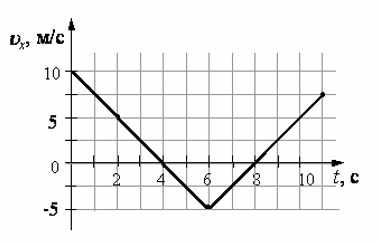
Ответ: 20.
Решение:
Путь, пройденный телом равен площади под соответствующим графиком зависимости модуля скорости тела от времени движения. Так как тело движется по оси х, других составляющих скорости, кроме υx у тела нет.
Площадь образовавшегося под графиком треугольника равна:
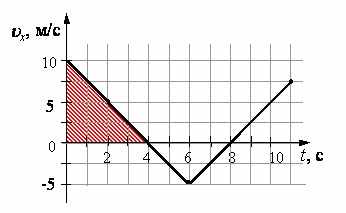
Задание 6
На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите ускорение тела.
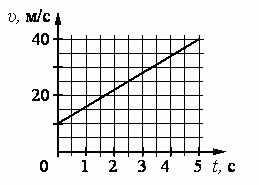
Ответ: 6 м/с2
Решение: Модуль ускорения автомобиля равен м/с2.
Задание 7
По графику зависимости скорости от времени (см. рисунок) определите ускорение прямолинейно движущегося тела в момент времени 2 с.
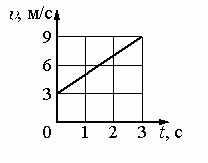
Ответ: 2 м/с2.
Решение: Так как движение равноускоренное, то ускорение постоянная величина и в момент времени 2 с ускорение такое же как и в момент времени 3 с. Определяем ускорение по формуле: м/с2.
Задание 8
Зависимость пути от времени прямолинейно движущегося тела имеет вид: x(t) = –4t + 10t2, где все величины выражены в СИ. Чему равно ускорение тела?
Ответ: 20 м/с2.
Ускорение есть вторая производная координаты по времени. Имеем м/с2.
Задание 9
Тело начинает падать из состояния покоя и перед ударом о Землю имеет скорость 80 м/с. Каково время падения? Сопротивлением воздуха пренебречь.
Ответ: 8с.
Решение: Все тела, падающие на Землю из состояния покоя, движутся с ускорением свободного падения g = 10 м/с2. Скорость падающего тела равна v(t) = v0 + gt, так как начальной скорости у тела нет (v0 =0), то время падения тела равно:
отсюда отсюда с.
Задание 10
Автомобиль трогается с места и движется с постоянным ускорением 5 м/с2. Какой путь прошёл автомобиль, если его скорость в конце пути оказалась равной 15 м/с?
Ответ: 22,5 м.
Решение: Пройденный автомобилем путь равен , где a ― ускорение автомобиля, равное a = 5 м/с2, t ― время его движения. Скорость автомобиля равна v(t) = at. Согласно условию, начальной скорости движения автомобиля нет.
Определим время, которое понадобилось автомобилю, чтобы развить конечную скорость v = 15 м/с:
Автомобиль прошел путь: м.
Задание 11.
При равноускоренном движении автомобиля на пути 25 м его скорость увеличилась от 5 до 10 м/с. Чему равно ускорение автомобиля?
Ответ: 1,5 м/с2.
Решение: Уравнение движения автомобиля , где v0 ― начальная скорость автомобиля v0 = 5 м/с, а ―постоянное ускорение автомобиля, t ― время движения автомобиля, S = 25 м.
Скорость автомобиля равна v = v0 + at, конечная скорость равна v = 10 м/с. Выразим из этого уравнения время движения автомобиля:
И определим ускорение из уравнения движения:
м/с2.
Задание 12.
Скорость пули при вылете из ствола пистолета равна 250 м/с. Длина ствола 0,1 м. Каково ускорение пули в конце ствола, если считать ее движение равноускоренным? Ответ выразить в км/с2.
Ответ: 312,5 км/с2.
Решение: Уравнение движения пули , где v0 ― начальная скорость пули v0 = 0 м/с, а ―постоянное ускорение пули, t ― время движения пули в стволе, S = 0,1 м ― путь, который проходит пуля в стволе.
Скорость пули при вылете из ствола считается по формуле v = v0 + at и равна по условию v = 250 м/с. Отсюда, время движения пули равно , а пройденный пулей путь:
Отсюда, ускорение пули равно:
м/с2 или 312,5 км/с2.
Таким образом, теперь вы сможете решать задания ЕГЭ по физике на темы равномерное прямолинейное движение и равноускоренное прямолинейное движение.