Простой множитель это множитель, который представляет собой простое число.

Любое составное число можно представить в виде произведения простых чисел.
Пример. Представим в виде произведения простых множителей числа 4, 6 и 8:
4 = 2 ·, 2,
6 = 2 ·, 3,
8 = 2 ·, 2 ·, 2.
Правые части полученных равенств называются разложением на простые множители.
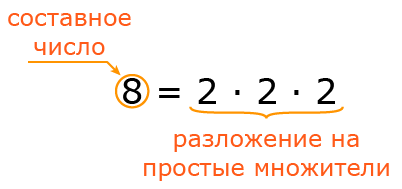
Разложение на простые множители это представление составного числа в виде произведения простых множителей.
Разложить составное число на простые множители значит представить это число в виде произведения простых множителей.
Простые множители в разложении числа могут повторяться. Повторяющиеся простые множители можно записывать более компактно в виде степени.
Пример.
24 = 2 ·, 2 ·, 2 ·, 3 = 23 ·, 3.
Примечание. Простые множители обычно записывают в порядке их возрастания.
Как разложить число на простые множители
Последовательность действий при разложении числа на простые множители:
- Проверяем по таблице простых чисел, не является ли данное число простым.
- Если нет, то последовательно подбираем самое маленькое простое число из таблицы простых чисел, на которое данное число делится без остатка, и выполняем деление.
- Проверяем по таблице простых чисел, не является ли полученное частное простым числом.
- Если нет, то последовательно подбираем самое маленькое простое число из таблицы простых чисел, на которое полученное частное делится нацело, и выполняем деление.
- Повторяем пункты 3 и 4 до тех пор, пока в частном не получится единица.
Пример. Разложите число 102 на простые множители.
Решение:
Начинаем поиск наименьшего простого делителя числа 102. Для этого последовательно подбираем самое маленькое простое число из таблицы простых чисел, на которое 102 разделится без остатка. Берём число 2 и пробуем разделить на него 102, получаем:
102 : 2 = 51.
Число 102 разделилось на 2 без остатка, поэтому 2 первый найденный простой множитель. Так как делимое равно делителю, умноженному на частное, то можно написать:
102 = 2 ·, 51.
Переходим к следующему шагу. Проверяем по таблице простых чисел, не является ли полученное частное простым числом. Число 51 составное. Начиная с числа 2, подбираем из таблицы простых чисел наименьший простой делитель числа 51. Число 51 не делится нацело на 2. Переходим к следующему числу из таблицы простых чисел (к числу 3) и пробуем разделить на него 51, получаем:
51 : 3 = 17.
Число 51 разделилось на 3, поэтому 3 второй найденный простой множитель. Теперь мы можем и число 51 представить в виде произведения. Этот процесс можно записать так:
102 = 2 ·, 51 = 2 ·, 3 ·, 17.
Проверяем по таблице простых чисел, не является ли полученное частное простым числом. Число 17 простое. Значит наименьшим простым числом, на которое делится 17, будет само это число:
17 : 17 = 1.
Так как в частном у нас получилась единица, то разложение закончено. Таким образом, разложение числа 102 на простые множители имеет вид:
102 = 2 ·, 3 ·, 17.
Ответ: 102 = 2 ·, 3 ·, 17.
В арифметике имеется ещё другая форма записи, облегчающая процесс разложения составных чисел. Она состоит в том, что весь процесс разложения записывают столбиком (в две колонки, разделённые вертикальной чертой). Слева от вертикальной черты, сверху вниз, записывают последовательно: данное составное число, затем получающиеся частные, а справа от черты соответствующие наименьшие простые делители.
Пример. Разложить на простые множители число 120.
Решение:
Пишем число 120 и справа от него проводим вертикальную черту:
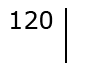
Справа от черты записываем самый маленький простой делитель числа 120:
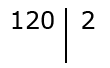
Выполняем деление и получившееся частное (60) записываем под данным числом:
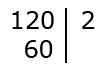
Подбираем наименьший простой делитель для 60, записываем его справа от вертикальной черты под предыдущим делителем и выполняем деление. Продолжаем процесс до тех пор, пока в частном не получится единица:
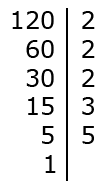
В частном у нас получилась единица, значит разложение закончено. После разложения в столбик множители следует выписать в строчку:
120 = 23 ·, 3 ·, 5.
Ответ: 120 = 23 ·, 3 ·, 5.
Составное число разлагается на простые множители единственным образом.
Это значит, что если, например, число 20 разложилось на две двойки и одну пятёрку, то оно и всегда будет так разлагаться независимо от того, начнём ли мы разложение с малых множителей или с больших. Принято начинать разложение с малых множителей, т. е. с двоек, троек и т. д.
Калькулятор разложения на множители
Данный калькулятор поможет вам выполнить разложение числа на простые множители. Просто введите число и нажмите кнопку Разложить.
| Разложить |