Шар и сфера это прежде всего геометрические фигуры, и если шар это геометрическое тело, то сфера это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.
Впоследствии когда было открыто, что Земля это шар, а небо небесная сфера, получило развитие новое увлекательное направление в геометрии геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.
Шар
Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара мы будем рассматривать его поверхность или оболочку шара.
 Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры круга.
Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры круга.
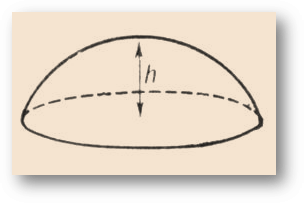
 Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.
Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.
В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.
Сфера
Сферой иначе называется поверхность шара. Сфера это не тело это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.
 Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.
Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.
Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.
Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе секущая к сфере содержит в себе ее хорду.
Объем шара
Формула для вычисления объема шара имеет вид:
V=4/3 πR3,
где R радиус шара.
Если нужно найти объем шарового сегмента воспользуйтесь формулой:
V сег=πh2(R-h/3), h высота шарового сегмента.
 Площадь поверхности шара или сферы
Площадь поверхности шара или сферы
Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):
S=4πR,
где R радиус сферы.
Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар