Возведение произведения в степень
Выражение (ab)n является степенью произведения множителей a и b. Это выражение можно представить в виде произведения степеней anbn. Докажем это на примере.
По определению степени:

Раскрываем скобки, а затем, используя переместительный закон умножения, переставляем сомножители так, чтобы одинаковые буквы стояли рядом:
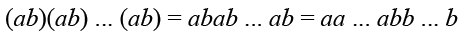
Группируем отдельно множители a и множители b и получаем:

Воспользовавшись определением степени, находим:

Следовательно, формула возведения произведения в степень будет выглядеть так:
(ab)n = anbn.
Свойство степени произведения распространяется на степень произведения двух и более множителей:
(3a2b)2 = 9a4b2.
Отсюда следует правило:
Чтобы возвести произведение в степень, можно отдельно возвести в эту степень каждый множитель и полученные результаты перемножить.
Возведение частного в степень
Для возведения в степень частного надо возвести в степень отдельно делимое и делитель.
Если говорить иначе, то степень частного равна частному степеней:
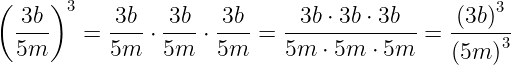
Так как частное в алгебре часто записывается в виде дроби (знак деления заменяется дробной чертой), то правило возведения частного в степень можно переформулировать так, чтобы оно подходило и для дробей:
Чтобы возвести дробь в степень надо возвести в эту степень отдельно её числитель и знаменатель.
Общая формула возведения в степень частного будет выглядеть так:
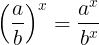
Возведение степени в степень
Для возведения степени числа в степень, надо перемножить показатели степеней, а основание оставить без изменений.
Например, нам нужно возвести 72 в третью степень:
(72)3.
Чтобы нам не возводить 7 сначала во вторую степень, а после этого ещё в третью, вспоминаем, что степень числа это сокращённая форма умножения одинаковых сомножителей, а это значит, что:
(72)3 = 72 ·, 72 ·, 72 = 72+2+2 = 72·,3 = 76.
Следовательно, при возведении степени в степень показатели степеней перемножаются.
Общая формула возведения степени в степень:
(ax)y = axy.
Примеры на свойства степеней
Пример 1. Выполните действия:
а) (x5)3,
б) 2(n3)5,
в) -4(a4)2.
Решение:
а) (x5)3 = x5 ·, 3 = x15,
б) 2(n3)5 = 2n3 ·, 5 = 2n15,
в) -4(a4)2 = -4a4 ·, 2 = -4a8.
Пример 2. Возведите в степень:
а) (-2mn)4,
б) (3bc)3,
в) (-6a4b)2.
Решение:
а) (-2mn)4 = (-2)4 ·, m4 ·, n4 = 16m4n4,
б) (3bc)3 = 33 ·, b3 ·, c3 = 27b3c3,
в) (-6a4b)2 = (-6)2 ·, (a4)2 ·, b2 = 36 ·, a8 ·, b2 = 36a8b2.
Пример 3. Возведите дробь в степень:
| а) ( | 2a | )2 | , |
| 5 |
| б) (- | xy | )5 | , |
| z |
| в) ( | a2b | )3 | . |
| 2c3 |
Решение:
| а) ( | 2a | )2 = | (2a)2 | = | 4a2 | , |
| 5 | 52 | 25 |
| б) (- | xy | )5 = — | (xy)5 | = — | x5y5 | , |
| z | z5 | z5 |
| в) ( | a2b | )3 = | (a2b)3 | = | (a2)3 ·, b3 | = | a6b3 | . |
| 2c3 | (2c3)3 | 23 ·, (c3)3 | 8c9 |