Теорема Пифагора:
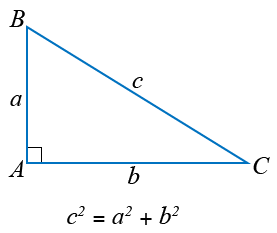
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Если A = 90, то a2 + b2 = c2.
Доказательство:
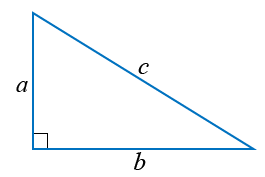
Возьмём прямоугольный треугольник с катетами a, b и гипотенузой c:
Достроим этот треугольник до квадрата со стороной a + b:
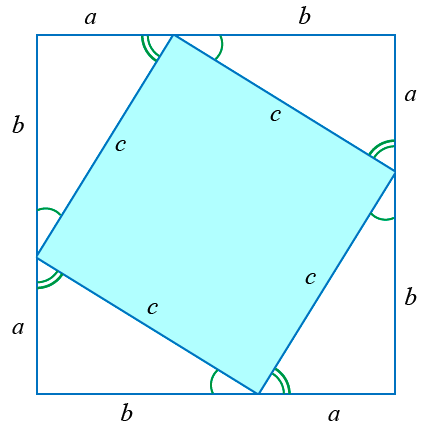
Площадь данного квадрата S будет равна (a + b)2:
S = (a + b)2.
С другой стороны, площадь этого квадрата состоит из четырёх одинаковых треугольник, площадь каждого из которых равна половине произведения их катетов (ab : 2), и квадрата со стороной c, поэтому:
S = (a + b)2
или
| S = 4 ·, ( | ab | ) + c2 = 2ab + c2 |
| 2 |
Таким образом:
(a + b)2 = 2ab + c2.
Так квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(a + b)2 = a2 + 2ab + b2,
то для того, чтобы наше равенство было верным c2 должен быть равен a2 + b2. Таким образом,
(a + b)2 = 2ab + c2, где c2 = a2 + b2.
Теорема доказана.
Обратная теорема Пифагора
Обратная теорема Пифагора:
Если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других сторон, то этот треугольник прямоугольный.
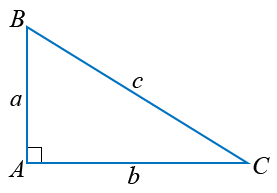
Если a2 + b2 = c2, то треугольник ABC прямоугольный.
Доказательство:
Возьмём треугольник ABC со сторонами a, b и c, у которого c2 = a2 + b2. Докажем, что A = 90:

Рассмотрим прямоугольный треугольник A1B1C1 с прямым углом A1, у которого A1B1 = a и A1C1 = b:
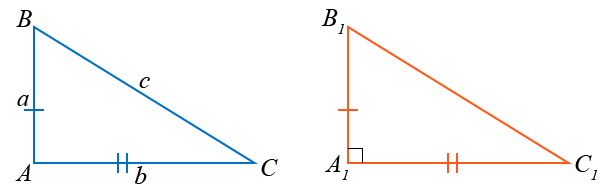
По теореме Пифагора:
B1C12 = A1B12 + A1C12.
Значит B1C12 = a2 + b2. Но a2 + b2 = c2 по условию теоремы. Следовательно B1C12 = c2, откуда можно сделать вывод B1C1 = c.
Треугольники ABC и A1B1C1 равны по трём сторонам, поэтому A = A1 = 90, то есть треугольник ABC является прямоугольным. Теорема доказана.