Теорема Виета

Теорема Виета:

Сумма корней приведённого квадратного уравнения

x2 + px + q = 0

равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену

x1 + x2 = -p, x1 &middot, x2 = q.

Доказательство:

Если приведённое квадратное уравнение имеет вид

x2 + px + q = 0,

то его корни равны:

,

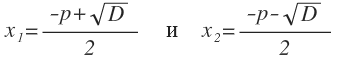где D = p2 — 4q. Чтобы доказать теорему, сначала найдём сумму корней:

,

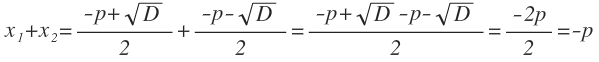а теперь найдём их произведение:

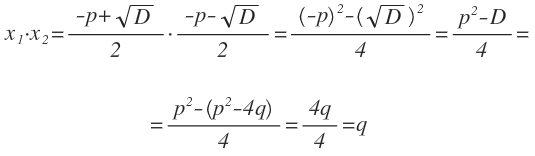
Равенства, показывающие зависимость между корнями и коэффициентами квадратного уравнения:

x1 + x2 = -p,

x1 &middot, x2 = q

называются формулами Виета.

Примечание: если дискриминант равен нулю (D = 0), то подразумевается, что уравнение имеет не один корень, а два равных корня.

Обратная теорема

Теорема:

Если сумма двух чисел равна -p, а их произведение равно q, то эти числа являются корнями приведённого квадратного уравнения:

x2 + px + q = 0.

Доказательство:

Пусть дано x1 + x2 = -p, значит, x2 = -p — x1. Подставим это выражение в равенство x1 &middot, x2 = q, получим:

x1(-p — x1) = q,

-px1 — x12 = q,

x12 + px1 + q = 0.

Это доказывает, что число x1 является корнем уравнения x2 + px + q = 0. Точно так же можно доказать, что и число x2 является корнем для этого уравнения.

Решение примеров

Зависимость между корнями и коэффициентами квадратного уравнения позволяет в некоторых случаях находить корни уравнения устно, не используя формулу корней.

Пример 1. Найти корни уравнения:

x2 — 3x + 2 = 0.

Решение: Так как

x1 + x2 = -(-3) = 3,

x1 &middot, x2 = 2,

очевидно, что корни равны 1 и 2:

1 + 2 = 3,

1 &middot, 2 = 2.

Подставив числа 1 и 2 в уравнение, убедимся, что корни найдены правильно:

12 — 3 &middot, 1 + 2 = 0

и

22 — 3 &middot, 2 + 2 = 0.

Ответ: 1, 2.

Пример 2. Найти корни уравнения:

x2 + 8x + 15 = 0.

Решение:

x1 + x2 = -8,

x1 &middot, x2 = 15.

Методом подбора находим, что корни равны -3 и -5:

-3 + -5 = -8,

-3 &middot, -5 = 15.

Ответ: -3, -5.

С помощью теоремы, обратной теореме Виета, можно составлять квадратное уравнение по его корням.

Пример 1. Составить квадратное уравнение по его корням:

x1 = -3, x2 = 6.

Решение: Так как x1 = -3, x2 = 6 корни уравнения x2 + px + q = 0, то по теореме, обратной теореме Виета, составим уравнения:

p = -(x1 + x2) = -(-3 + 6) = -3,

q = x1 &middot, x2 = -3 &middot, 6 = -18.

Следовательно, искомое уравнение:

x2 — 3x — 18 = 0.

Ответ: x2 — 3x — 18 = 0.

Пример 2. Записать приведённое квадратное уравнение, имеющее корни:

x1 = 2, x2 = 3.

Решение:

p = -(x1 + x2) = -(2 + 3) = -5,

q = x1 &middot, x2 = 2 &middot, 3 = 6.

Ответ: x2 — 5x + 6 = 0.