Решающую роль в решении задач на тригонометрию играет знание определений тригонометрических функций.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Рассмотрим прямоугольный треугольник ABC и угол A в нем.
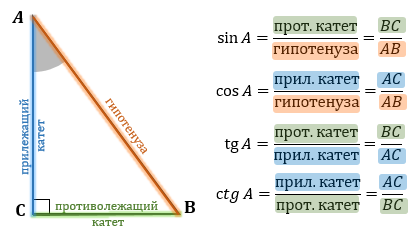
Синус угла — отношение противолежащего катета к гипотенузе.
Косинус угла — отношение прилежащего катета к гипотенузе.
Тангенс угла — отношение противолежащего катета к прилежащему.
Котангенс угла — отношение прилежащего катета к противолежащему.
Как найти синус, косинус, тангенс, котангенс в треугольнике
В треугольнике ABC c углом С, равным 90°, гипотенуза AB = 17, а катет AC = 15.
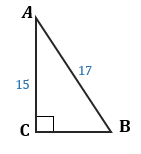
Нужно найти синус, косинус, тангенс, котангенс в данном треугольнике.
Найдем синус угла B:
Чтобы найти косинус угла B, необходимо значение прилежащего катета — BC, которое нам пока неизвестно. Из Пифагоровой тройки 8 : 15 : 17 находим BC = 8.
Найдем тангенс угла B:
Найдем котангенс угла B:
.
Найдем синус угла A:
,
Заметим, что . Аналогично, получим:
.
Можно запомнить эту закономерность. Это происходит, потому что и тут вступают в силу формулы приведения, которые более подробно будут в дальнейшем разобраны.
Тригонометрические функции безразмерные величины.
Важно понимать, что тригонометрические функции — это безразмерные величины(не имеют единиц измерения), они показывают только отношение.
К примеру, если для треугольника ABC известно, что , это не значит, что противолежащий углу B катет AC равен , это не значит, что противолежащий углу B катет AC равен , а гипотенуза AB равна 2. Это значит, что противолежащий катет AC относится к гипотенузе AB как к 2.
И если бы нам была известна одна из длин: либо катет AC, либо гипотенуза AB — то, зная синус угла B, мы могли бы найти вторую сторону.
Формулы
В ЕГЭ тригонометрия формулы имеет простые. Нет сложных задач, не нужно доказывать тригонометрические тождества и решать тригонометрические неравенства.
Приведем основные формулы по тригонометрии.
Это, конечно, основное тригонометрическое тождество:
. На самом деле, если мы посмотрим на треугольник и на те выражения, которые мы записали для синуса и косинуса одного угла в нем, то получим:
Итак, теперь вы знаете основное тригонометрическое тождество. Формулы тригонометрии в основном выводятся из него. Вот основные из них:

Удачи на экзаменах. Посмотрите еще интересные темы: экономические задачи ЕГЭ, задачи по теории вероятности.