Умножение
Умножение десятичных дробей сводится к умножению соответствующих натуральных чисел, и правильному определению места запятой в полученном результате.
Пример. Найти произведение чисел 2,13 и 1,2.
Решение: можно перемножить числа 2,13 и 1,2, заменив их обыкновенными дробями:
| 2,13 ·, 1,2 | = | 2 | 13 | ·, | 1 | 2 | = | 213 | ·, | 12 | = |
| 100 | 10 | 100 | 10 |
| = | 213 ·, 12 | = | 2556 | = 2,556. |
| 100 ·, 10 | 1000 |
Можно сказать, что мы перемножили натуральные числа, которые получатся если у данных десятичных дробей отбросить запятые. Так как знаменатели тоже перемножаются, то в знаменателе вышло число с тремя нулями, а в соответствующей десятичной дроби три цифры после запятой. Значит в результате умножения двух десятичных дробей, ответ будет содержать столько знаков после запятой, сколько их было в обоих множителях вместе.
Данное произведение можно посчитать и столбиком, заменив дроби на натуральные числа:

Из рассмотренного примера можно сделать вывод, что:
Чтобы перемножить две десятичные дроби, достаточно перемножить их как натуральные числа, и в полученном произведении отделить справа запятой столько знаков, сколько их было в множимом и множителе вместе.
Данное правило работает и для умножения десятичной дроби на натуральное число. Только в случае, когда один из множителей натуральное число, количество десятичных знаков в результате будет равно количеству знаков дробного множителя.
Пример. Найти произведение чисел 4,324 и 11:
Решение:
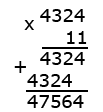
4,324 ·, 11 = 47,564.
Деление
Чтобы разделить десятичную дробь на целое число, нужно сначала разделить целую часть (если она есть), затем поставить запятую в неполном частном и приступить к делению дробной части:
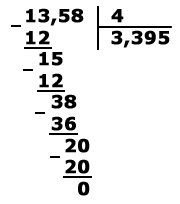
В этом примере мы сначала разделили 13 на 4 и записали в частное 3, затем мы поставили в частном запятую, так как у нас в остатке осталась единица, которую на 4 мы уже поделить не могли, затем мы продолжили делить дробную часть. Особенность этого примера заключается в том, что когда мы получили в частном 9 сотых, то обнаружили остаток, равный 2 сотым, мы раздробили этот остаток на тысячные доли, получили 20 тысячных и довели деление до конца.
Чтобы разделить десятичную дробь (или целое число) на десятичную дробь, нужно в делимом и в делителе перенести запятую на столько цифр вправо, сколько их после запятой в делителе, после чего выполнить деление по правилу деления на целое число.
В качестве примера разделим 72,9 на 0,09:
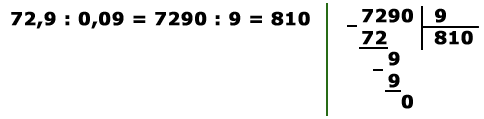
Также можно осуществить деление десятичной дроби (или целого числа) на десятичную дробь, представив оба числа в виде обыкновенных дробей:
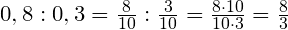
Таким образом, частное двух десятичных дробей всегда можно записать в виде обыкновенной дроби.