Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить.
Произведением двух многочленов будет многочлен.
Пример 1. Выполните умножение многочленов a + 5 и a — 2.
Решение: Составим произведение многочленов и раскроем скобки:
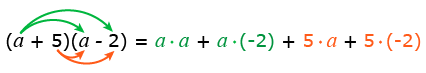
Выполним умножение, руководствуясь правилом умножения одночленов, соблюдая правило знаков при умножении и правило умножения степеней:
a ·, a + a ·, (-2) + 5 ·, a + 5 ·, (-2) = a2 — 2a + 5a — 10.
Полученный в результате многочлен можно упростить, выполнив приведение подобных членов:
a2 — 2a + 5a — 10 = a2 + 3a — 10.
Пример 2. Запишите степень двучлена в виде произведения и выполните умножение:
(a — b)2.
Решение: Сначала запишем степень в виде произведения. Так как вторая степень выражения это умножение этого выражения самого на себя, то квадрат разности в виде произведения будет выглядеть так:
(a — b)(a — b).
Теперь раскроем скобки и выполним умножение:
(a — b)(a — b) = aa — ab — ab + bb = a2 — ab — ab + b2.
Сделаем приведение подобных членов:
a2 — ab — ab + b2 = a2 — 2ab + b2.
Пример 3. Представьте в виде многочлена:
(x — 1)(x2 + 2x — 1).
Решение: Сначала умножим каждый член первого многочлена на каждый член второго многочлена (раскроем скобки):
(x — 1)(x2 + 2x — 1) = x3 + 2×2 — x — x2 — 2x + 1.
Так как в получившемся многочлене есть подобные члены, мы можем упростить его с помощью приведения подобных членов:
x3 + 2×2 — x — x2 — 2x + 1 = x3 + x2 — 3x + 1.