Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.
При умножении одночлена на многочлен используется распределительное свойство умножения:
a(b + c) = ab + ac,
правило умножения степеней с одинаковыми основаниями:
ax ·, ay = ax + y
и правило знаков при умножении.
Произведением одночлена и многочлена будет многочлен.
Пример 1. Умножить одночлен -5a на многочлен 3a + 4b2.
Решение: Составим произведение одночлена и многочлена и с помощью распределительного свойства умножения раскроем скобки:
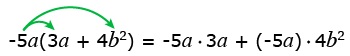
Теперь осталось выполнить умножение одночленов друг на друга:
-5a ·, 3a + (-5a) ·, 4b2 = -15a2 — 20ab2.
Так как в получившемся результате нет подобных членов, то многочлен -15a2 — 20ab2 это окончательный результат умножения одночлена -5a на многочлен 3a + 4b2.
Пример 2. Выполните умножение многочлена x — xy + 2 на одночлен 2y.
Решение: Составим произведение многочлена и одночлена:
(x — xy + 2)2y.
Для удобства можно записать одночлен перед многочленом, используя переместительное свойство умножения. После этого раскроем скобки:
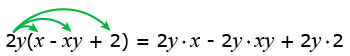
Теперь надо перемножить одночлены:
2y ·, x — 2y ·, xy + 2y ·, 2 = 2xy — 2xy2 + 4y.
Решение данного примера можно записать короче, не выписывая промежуточные результаты:
(x — xy + 2)2y = 2xy — 2xy2 + 4y.
Пример 3. Упростите выражение:
3×2 — x(4x — 6y).
Решение: Раскроем скобки, выполнив умножение -x на 4x — 6y, и затем сделаем приведение подобных членов (если они будут):
3×2 — x(4x — 6y) = 3×2 — 4×2 + 6xy = -1×2 + 6xy.
Так как получившийся в результате многочлен является алгебраической суммой, то его можно записать так:
6xy — 1×2.