Виды углов

Каждый угол, в зависимости от его величины, имеет своё название:

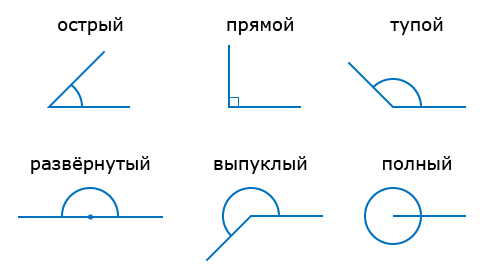
• Острый угол это угол, который меньше прямого угла (&lt,90).
• Прямой угол это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90.

  Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:

  

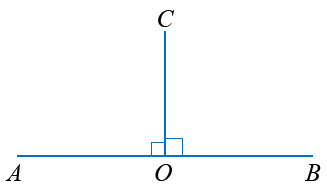
  AOC и COB прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O основанием перпендикуляра.

  Сумма двух прямых углов равна развёрнутому углу, значит, прямой угол равен половине развёрнутого угла.
  
  
  
  

• Тупой угол это угол, который больше прямого угла, но меньше развёрнутого:

  90 &lt, тупой угол &lt, 180.

• Развёрнутый угол это угол, образованный двумя дополнительными лучами.

  Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180 или 2d.

  Все развёрнутые углы равны между собой.

  
  
  

• Выпуклый угол это угол, который больше развёрнутого угла, но меньше полного:

  180 &lt, выпуклый угол &lt, 360.
• Полный угол это угол, обе стороны которого совпадают с одним лучом.

  Полный угол равен сумме четырёх прямых углов, то есть 4d (360).
  
  

Прилежащие углы

Прилежащие углы это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.

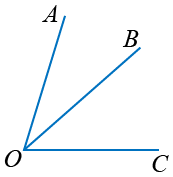
AOB и BOC прилежащие углы, O общая вершина, OB общая сторона.

Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.

Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:

AOB = AOC + COB.

Каждый из прилежащих углов, AOC и COB, называется разностью углов AOB и другого прилежащего, то есть:

AOC = AOB — COB,

COB = AOB — AOC.