Внешний угол треугольника это угол, смежный с любым из внутренних углов треугольника.
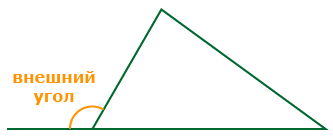
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
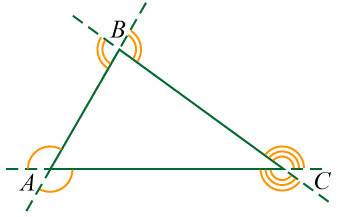
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
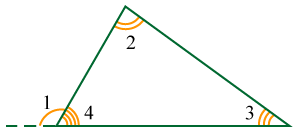
Так как внешний угол (1) дополняет внутренний угол (4) до развёрнутого угла, то их сумма равна 180:
1 + 4 = 180.
Сумма внутренних углов углов любого треугольника тоже равна 180, значит:
2 + 3 + 4 = 180.
Из этого следует, что
1 + 4 = 2 + 3 + 4.
Сократив обе части полученного равенства на одно и тоже число (4), получим:
1 = 2 + 3.
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360
Рассмотрим треугольник ABC:
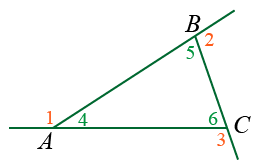
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540:
(1 + 4) + (2 + 5) + (3 + 6) = 180 + 180 + 180 = 540.
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
1 + 2 + 3 = 540 — (4 + 5 + 6) = 540 — 180 = 360.