Вписанный угол окружности это угол, образованный двумя хордами, исходящими из одной точки, то есть вписанным углом называется угол, вершина которого лежит на окружности.

Угол ABC вписанный угол. ABC опирается на дугу AC, заключённую между его сторонами.
Теорема о вписанном угле
Теорема:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Это следует понимать так: вписанный угол содержит в два раза меньше градусов, чем дуга, на которую он опирается:

| ABC = | 1 | AC. |
| 2 |
Доказательство:
При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности.
Первый случай. Сторона вписанного угла проходит через центр окружности.
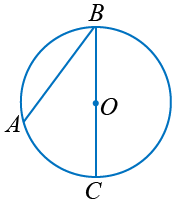
Соединим точку A с центром круга (точкой O). Получим равнобедренный треугольник AOB, в котором AO = OB, как радиусы одной окружности. Следовательно, A = B, как углы при основании равнобедренного треугольника.

Так как AOC внешний угол равнобедренного треугольника, то:
AOC = A + B,
а так как углы A и B равны, то
| B = | 1 | AOC. |
| 2 |
Но AOC центральный угол, значит AOC = AC, следовательно B измеряется половиной дуги AC:
| ABC = B = | 1 | AC. |
| 2 |
Второй случай. Центр окружности лежит между сторонами вписанного угла.

Проведём диаметр BD. Угол ABC разбился на два угла: 1 и 2.
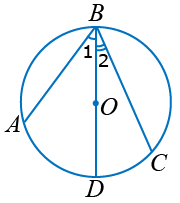
Точка D разделяет дугу AC на две дуги: AD и DC. По доказательству, рассмотренному в первом случае:
| 1 = | 1 | AD и 2 = | 1 | DC. |
| 2 | 2 |
Следовательно, весь угол ABC будет измеряться половиной дуги AC:
| 1 + 2 = | 1 | AD + | 1 | DC |
| 2 | 2 |
или
| ABC = | 1 | AC. |
| 2 |
Третий случай. Центр окружности лежит вне вписанного угла.

Проведём диаметр BD.
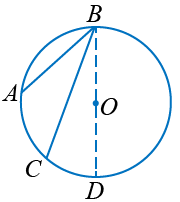
ABC = ABD — CBD.
Но ABD измеряется половиной дуги AD , а CBD измеряется половиной дуги CD. Следовательно,
| ABC = | 1 | (AD — CD), |
| 2 |
то есть
| ABC = | 1 | AC. |
| 2 |
Следствия из теоремы
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги.

2. Вписанный угол, опирающийся на диаметр, прямой, так как он опирается на половину окружности.
Половина окружности содержит 180, значит, угол, опирающийся на диаметр, содержит 90.
