Задачи на движение

Задачи на движение начинают проходить в 5 классе и решают все оставшиеся учебные годы вплоть до 11 класса. В ЕГЭ по математике вы найдете задачи на движение в задании 11, в котором собраны все текстовые задачи. Рассмотрим как надо решать задачи на движение из ЕГЭ. Но сначала немного теории.

Как решать задачи на движение

Решение задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:

1. Анализ данных.
2. Составление таблицы.
3. Составление уравнения.
4. Решение уравнения.

Остановимся подробно на каждом пункте:

1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.

Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.

2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.

Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:

S = v · t.

В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.

3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.

По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.

4. Решить полученное уравнение и прийти к ответу.

Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.

Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения. Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.

Примеры решения

Пример:

Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

Решение:

В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:

	v, км/ч	t, ч	S, км
Первый велосипедист	x + 10		60
Второй велосипедист	x		60

В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:

3×2 + 90x = 600 + 60x,

x2 + 10x – 200 = 0.

Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.

Ответ: 10 км/ч.

Виды задач на движение

Движение навстречу друг другу, движение в противоположных направлениях

Если два объекта движутся навстречу друг другу, то они сближаются:

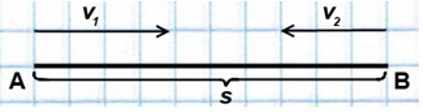
При движении в противоположном направлении объекты удаляются:

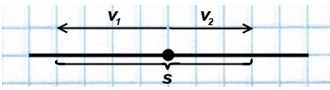
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:

v = v1 + v2.

Движение друг за другом (вдогонку)

При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.

Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

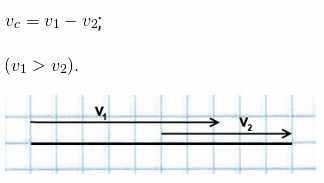
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

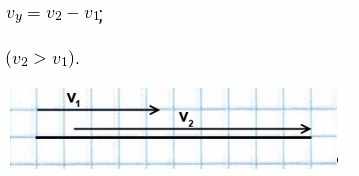
Таким образом:

При движении навстречу друг другу и движении в противоположных направлениях скорости складываем. При движении в одном направлении скорости вычитаем.

Задачи на движение по кругу

При движении по кругу объекты могут:

• сближаться, если скорость догоняющего больше скорости догоняемого. Скорость сближения будет равна ,
• отдаляться, если скорость догоняющего меньше скорости догоняемого. Скорость удаления будет равна .

При этом пройденные расстояния измеряются длиной круговой трассы, равной S.

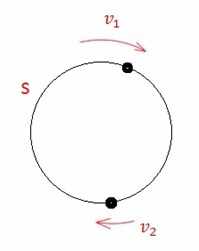
• Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
• Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0 км большее расстояние, чем догоняемый.
• Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S:   S1 – S2 = m · S.

Задачи на движение мимо объекта

В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.

Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:

S = L = v0 · t.

При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).

Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта: S = L1 + L2 = v0 · t.

При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.

Задачи на движение по течению и против течения

В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.

При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.

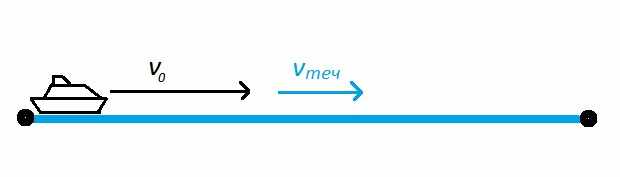
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.

Задачи на движение из ЕГЭ по математике (профильный уровень)

Задача 1.

Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение: Пусть скорость второго автомобиля равна v км/ч. За 4/5 часа первый автомобиль прошел на 44 км больше, чем второй, отсюда имеем:

112 ∙ = v ∙ = v ∙ + 44 ⇔ 4 ∙ v = 112 ∙ 4 – 44 ∙ 5 ⇔ v = 57.

Следовательно, скорость второго автомобиля была равна 57 км/ч.

Ответ: 57 км/ч.

Задача 2.

Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.

Решение:

До первой встречи велосипедист провел на трассе 1/5 часа, а мотоциклист 1/30 часа. Пусть скорость мотоциклиста равна v км/ч, тогда скорость велосипедиста равна

Тогда если скорость велосипедиста – это 1 единица отношения, то скорость мотоциклиста – это 6 единиц отношения.

Так как они едут в одном направлении, их общая скорость 5 единиц отношения.

∙5 ед.отн. = 5

1 ед.отн. = 20

6 ед.отн. = 120

Таким образом, скорость мотоциклиста была равна 120 км/ч.

Ответ: 120 км/ч.

Задача 3

Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Решение: Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой ― 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет L делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:

, отсюда , отсюда и .

Ответ: через 9 минут.

Задача 4

Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение:

Данную задачу можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т. к. сказано, что на один круг). Найти скорость второго. Очень важно в заданиях на движение представить сам процесс этого движения.

Сравнение так же производим по расстоянию.

За x принимаем искомую величину ― скорость второго. Время движения 40 минут (2/3 часа) для обоих. Заполним графу «расстояние»:

	v	t	S
1	80	2/3
2	x	2/3

Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.

80 ∙ больше, чем x ∙ больше, чем x ∙   на 14.

80 ∙ = x ∙ = x ∙ + 14,

– – = x ∙ ,

160 – 42 = х ∙ 2,

х = 59.

Скорость второго автомобиля 59 (км/ч).

Ответ: 59 км/ч.

Задача 5

Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.

Решение:

Пусть v км/ч – скорость велосипедиста, тогда скорость автомобилиста равна v + 40 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:

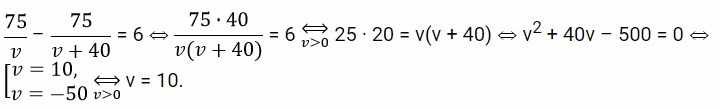
Таким образом, скорость велосипедиста была равна 10 км/ч.

Ответ: 10 км/ч.