Переместительный закон сложения
Если слагаемые поменять местами, то сумма не изменится. Это можно легко проверить, посчитав количество звёздочек, представленных на рисунке:
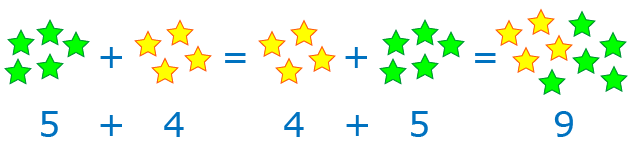
Можно сначала посчитать зелёные звёздочки, потом жёлтые и сложить полученные результаты, получится 9 звёздочек. Или можно сначала посчитать жёлтые звёздочки, а потом зелёные, в результате сложения жёлтых и зелёных звёздочек сумма будет опять равна 9.
Таким образом, для любых натуральных чисел a и b верно равенство:
a + b = b + a,
выражающее переместительный закон сложения:
От перестановки слагаемых сумма не меняется.
Сумма нескольких слагаемых
При сложении нескольких слагаемых действия можно выполнять в любом порядке.
Пример. Найти сумму трёх слагаемых: 5, 3 и 2.

Решение: Сумму трёх слагаемых можно найти тремя способами:

1-й способ:
5 + 3 = 8,
8 + 2 = 10.
2-й способ:
5 + 2 = 7,
7 + 3 = 10.
3-й способ:
3 + 2 = 5,
5 + 5 = 10.
Сочетательный закон сложения
Если при сложении чисел 5, 2 и 3 заменить какие-нибудь два числа их суммой, то результат сложения не измениться. Это можно легко проверить посчитав звёздочки на картинке:

Можно посчитать зелёные, синие и жёлтые звёздочки отдельно, а потом сложить полученные результаты, получим 10 звёздочек. Или можно посчитать зелёные звёздочки отдельно, а синие и жёлтые вместе и после к зелёным звёздочкам прибавить сумму синих с жёлтыми, в результате получим опять 10 звёздочек.
Из примера следует, что результат сложения не зависит от объединения слагаемых в сумму. Таким образом, для любых натуральных чисел a, b и c верно равенство:
a + b + c = a + (b + c) = b + (a + c)
выражающее сочетательный закон сложения:
Сумма трёх и более слагаемых не изменится, если какие-нибудь из них заменить их суммой.