Законы умножения

Переместительный закон умножения

Если множимое и множитель поменять местами, то произведение не изменится. Это можно легко проверить при подсчёте двумя способами числа звёздочек представленных на рисунке:

3 + 3 + 3 + 3 = 4 + 4 + 4

Так как множимое и множитель можно менять местами их ещё называют сомножителями или просто множителями.

Таким образом, для любых натуральных чисел a и b верно равенство:

a &middot, b = b &middot, a,

выражающее переместительный закон умножения:

От перестановки сомножителей произведение не меняется.

Сочетательный закон умножения

Произведение чисел 3, 2 и 4 не изменится, если из них какие-нибудь два числа заменить их произведением:

3 &middot, 2 &middot, 4 = 3 &middot, (2 &middot, 4) = 3 &middot, 8 = 24,

3 &middot, 2 &middot, 4 = (3 &middot, 2) &middot, 4 = 6 &middot, 4 = 24.

Таким образом, для любых натуральных чисел a, b и c верно равенство:

a &middot, b &middot, c = (a &middot, b) &middot, c = a &middot, (b &middot, c),

выражающее сочетательный закон умножения:

Произведение не изменится, если какую-либо группу сомножителей заменить их произведением.

Распределительный закон умножения

Для любых натуральных чисел верны равенства:

m &middot, (a + b + …) = m &middot, a + m &middot, b + …

(a + b + …) &middot, m = a &middot, m + b &middot, m + … ,

выражающие распределительный закон умножения:

Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

Распределительный закон умножения можно легко проверить при подсчёте двумя способами числа звёздочек, представленных на рисунке:

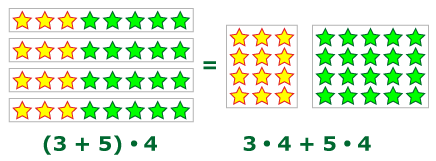
Первый: в каждом ряду расположено 3 жёлтых и 5 зелёных звёздочек, то есть всего в каждом ряду (3 + 5) звёздочек. В четырёх рядах всего (3 + 5) &middot, 4 звёздочек.

Второй: жёлтые звёздочки расположены в четыре ряда по 3 звёздочки в каждом, то есть всего жёлтых звёздочек 3 &middot, 4, а зелёных 5 &middot, 4. Всего звёздочек 3 &middot, 4 + 5 &middot, 4.

Кроме того, для любых натуральных чисел (если уменьшаемое больше или равно вычитаемому) верны равенства:

m &middot, (a — b — …) = m &middot, a — m &middot, b — …

(a — b — …) &middot, m = a &middot, m — b &middot, m — …

Например, 6 &middot, (4 — 2) = 6 &middot, 4 — 6 &middot, 2.

Переход от умножения:

m &middot, (a + b + …)

и

m &middot, (a — b — …)

соответственно к сложению и вычитанию:

m &middot, a + m &middot, b + …

и

m &middot, a — m &middot, b — …

называется раскрытием скобок.

Переход от сложения и вычитания:

m &middot, a + m &middot, b + …

и

m &middot, a — m &middot, b — …

к умножению:

m &middot, (a + b + …)

и

m &middot, (a — b — …)

называется вынесением общего множителя за скобки.