Как найти разность чисел в математике?

Вычесть значит отнять одно число от другого. Вычитание есть такое действие, в котором отнимают меньшее число от большего. При вычитании целых чисел большее число уменьшается на столько единиц, сколько их содержится в меньшем.

Вычесть одно число из другого значит убавить одно число другим, поэтому вычитание есть действие обратное сложению.

Вычитание

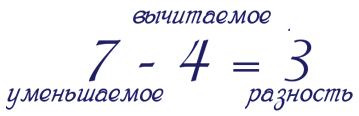
В вычитании два данных числа называются уменьшаемым и вычитаемым, а искомое — разностью.

Уменьшаемым называют большее число, от которого отнимают другое. Оно уменьшается от вычитания.

Вычитаемым называют меньшее число, которое отнимают от большего.

Разностью называют вывод, полученный от вычитания. Разность определяет, чем одно число больше другого или показывает разницу между двумя числами.

Знак вычитания. Действие вычитания обозначается знаком — (минус).

Вычитание однозначных чисел

Чтобы обозначить, что из 9 нужно вычесть 6, пишут эти числа рядом, отделяя их знаком — (минус):

• 9 6.

Разность между этими числами будет 3, и ход вычисления выражают словесно:

девять без шести равно трем.

Письменно:

• 9 6 = 3.

Большее число 9 будет уменьшаемым, меньшее 6 вычитаемым, число 3 остатком.

Способы вычитания

Можно двумя способами вычесть одно число из другого:

1. или можно отнять от большего числа столько единиц, сколько их содержится в меньшем. Так, из 9 вычесть 6 значит от 9 отнять 6. Число 3 будет искомый остаток,
2. или можно к меньшему числу прибавлять по единице до тех пор, пока не получим большее число. Так, вычитая 6 из 9, мы к 6 прибавляем 3 единицы.

Число единиц, которое нужно прибавить к меньшему числу, чтобы уравнять его с большим, определяет разность.

Меньшее число с разностью должно равняться большему числу, следовательно, меньшее число и разность суть слагаемые, а большее — их сумма. На этом основано другое определение вычитания:

• Вычитание есть такое действие, в котором по данной сумме и одному слагаемому отыскивается другое слагаемое.

В этом случае данная сумма есть уменьшаемое, данное слагаемое — вычитаемое, а искомаяразность — другое слагаемое.

Вычитание многозначных чисел

Вычитание многозначных чисел основывается на том свойстве чисел, по которому вычесть число все-равно, что вычесть все его части. Из этого свойства видно, что вычесть какое-нибудь число все-равно, что вычесть последовательно все его единицы, десятки, сотни и т. д. Чтобы обозначить, что из числа 7228 нужно вычесть 3517, пишут:

• 7228 3517 и вычитают отдельно единицы из единиц, десятки из десятков и т. д.

Чтобы облегчить вычитание, подписывают меньшее число под большим так, чтобы единицы одинаковых порядков находились в одном вертикальном столбце, проводят черту, слева ставят знак вычитания и под чертою подписывают разность.

Ход вычисления выражают словесно:

1. Начинаем вычитание с простых единиц: 8 без 7 составляют 1, подписывают под единицами 1.
2. Вычитаем десятки: 2 без 1 дают 1, подписываем под десятками 1.
3. Вычитаем сотни. Пять нельзя вычесть из 2, поэтому занимаем у следующего высшего порядка (тысяч) единицу, что и обозначаем тем, что над 7 ставим точку. Единица каждого порядка содержит 10 единиц следующего меньшего порядка. Присоединяя эти 10 единиц к 2, получим 12, 12 без 5 составляют 7, подписываем под сотнями 7. Когда занимают единицу у высшего порядка, обозначают это тем, что ставят точку над порядком, у которого занимают.
4. Вычитаем тысячи. Тысяч осталось вместо 7 только 6, ибо одна была взята. 6 без 3 составляют 3, подписываем под тысячами 3.

Ход вычисления выражают письменно:

Пример. Из 17004 вычесть 6025.

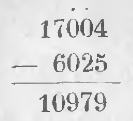
Из 4 нельзя вычесть 5. Занимаем единицу у десятков, следующего высшего порядка, но в этом порядке единиц нет, занимаем у сотен, и сотен нет, занимаем у тысяч и обозначаем это точкой над цифрой 7.

Единица четвертого имеет 10 единиц третьего порядка. Взяв из них одну для десятков, оставляем их в сотнях только 9. Присоединив 10 к 4, имеем 14.

Производя вычитание, получим:

• для единиц 14 5 = 9
• для десятков 9 2 = 7
• для сотен 9 0 = 9
• для тысяч 6 6 = 0

Для десятков тысяч имеем 1, ибо эту цифру уменьшаемого переносим в разность без изменения.

Ход вычисления выразится письменно:

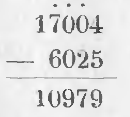
Из предыдущих примеров выводим правила вычитания:

1. Чтобы сделать вычитание целых чисел, нужно вычитаемое подписать под уменьшаемым так, чтобы единицы одинаковых порядков стояли в одном вертикальном столбце, провести черту, под которою и подписать разность.
2. Вычитание нужно начинать с простых единиц, то есть с первого столбца, и затем, переходя к следующим столбцам от правой руки к левой, вычитают десятки из десятков, сотни из сотен и т. д.
3. Если цифра вычитаемого меньше цифры уменьшаемого, разность подписывают в том же столбце, если цифры равны, разность будет нуль.
4. Если же цифра вычитаемого больше соответствующей цифры уменьшаемого, занимают единицу у следующего порядка уменьшаемого, отмечая это точкой, поставленной над цифрой, у которой занимают, прикладывают 10 к цифре уменьшаемого и производят вычитание. Цифру же с точкой считают на единицу меньше.
5. Если при вычитании цифра уменьшаемого, у которого занимают, будет 0, за которым в уменьшаемом следуют тоже нули, то занимают у первой значащей цифры, ставя над нею и всеми промежуточными нулями точки. Цифру с точкой считают на единицу меньше, а нули с точкой считают за 9.
6. Вычитание продолжают до тех пор, пока не получат полной разности.
7. Лишние цифры уменьшаемого переносят в разность.

Зависимость между данными и искомыми вычитания

Из примера 9 6 = 3 видно, что

1. Уменьшаемое равно вычитаемому, сложенному с разностью: 9 = 6 + 3.
2. Вычитаемое равно уменьшаемому без разности: 6 = 9 3.
3. Разность равна уменьшаемому без вычитаемого: 3 = 9 6.

Арифметическое дополнение. Разность между числом и ближайшей большей единицей называется арифметическим дополнением. Так, арифметическими дополнениями чисел 7, 79, 983 будут числа:

• 10 7 = 3
• 100 79 = 21
• 1000 983 = 17

Арифметическим дополнением иногда пользуются для облегчения арифметических вычислений.

Вычитание чисел

Вычитание – это арифметическое действие обратное сложению, посредством которого из одного числа вычитают (отнимают) столько единиц, сколько их содержится в другом числе.

Число, из которого вычитают, называется уменьшаемым, число, которое указывает сколько единиц будет вычтено из первого числа, называется вычитаемым. Число, получаемое в результате вычитания, называется разностью (или остатком).

Рассмотрим вычитание на примере. На столе лежит 9 конфет, если съесть 5 конфет, то их останется 4. Число 9 является уменьшаемым, 5 – вычитаемым, а 4 – остатком (разностью):

Для записи вычитания используется знак (минус). Он ставится между уменьшаемым и вычитаемым, при этом уменьшаемое записывается слева от знака минус, а вычитаемое – справа. Например, запись 9  5 означает, что из числа 9 вычитается число 5. Справа от записи вычитания ставят знак = (равно), после которого записывают результат вычитания. Таким образом, полная запись вычитания выглядит так:

Эта запись читается так: разность девяти и пяти равняется четырём или девять минус пять равно четыре.

Чтобы в результате вычитания получить натуральное число или 0, уменьшаемое должно быть больше вычитаемого или равно ему.

Рассмотрим, как, используя натуральный ряд, можно выполнить вычитание и найти разность двух натуральных чисел. Например, нам необходимо вычислить разность чисел 9 и 6, отметим в натуральном ряду число 9 и отсчитаем от него влево 6 чисел. Получим число 3:

9 6 = 3

Вычитание также можно использовать для сравнения двух чисел. Желая сравнить между собой два числа, мы задаёмся вопросом, на сколько единиц одно число больше или меньше другого.

Чтобы узнать это, надо из большего числа вычесть меньшее. Например, чтобы узнать, на сколько 10 меньше 25 (или на сколько 25 больше 10), надо из 25 вычесть 10.

Тогда найдём, что 10 меньше 25 (или 25 больше 10) на 15 единиц.

Проверка вычитания

Рассмотрим выражение

15 7 = 8

где 15 – это уменьшаемое, 7 – это вычитаемое, а 8 – разность. Чтобы узнать правильно ли было выполнено вычитание, можно:

1. вычитаемое сложить с разностью, если получится уменьшаемое, то вычитание было выполнено верно:7 + 8 = 15
2. от уменьшаемого отнять разность, если получится вычитаемое, то вычитание было выполнено верно:15 8 = 7

Что такое разность чисел в математике?

Для многих точные науки, вроде математики, воспринимаются как нечто более простое, чем сферы, требующие рассуждений, предполагающие большую вариативность. Однако все предметы имеют свои сложности, в том числе и технические.

Вычитание

Для того, чтобы понять, чем является разность, необходимо разобраться в ряде математической терминологии. В первую очередь, нужно выяснить, чем является вычитание.

По-другому это понятие называют убавлением, и по такому названию понять смысл процесса несколько проще. По своей сути вычитание является одной из математических операций.

Что же это за операции? Как правило, под ними понимают определенные арифметические или логические действия. Встает логичный вопрос – в чем же суть арифметических действий?

Понятие арифметики появилось достаточно давно. Оно зародилось в древнегреческом языке, где переводилось как «число». Сегодня это раздел математики, который изучает числа, их отношения друг к другу, а также свойства.

Итак, вычитание – это операции с числами, относящиеся к бинарным. Суть бинарных операций в том, что в них используются два аргумента (параметра), и получается один результат.

Стоит рассмотреть, как найти разность какого-то числа. В первую очередь, необходимы два аргумента, то есть два числа. Затем необходимо уменьшить значение первого числа на значение второго.

Когда данная операция выражается письменно, используется знак «минус». Это выглядит так: а – б = с, где а является первым числовым значением, б – вторым, а с – разностью чисел.

Как правило, у учеников возникает гораздо больше проблем именно с вычитанием, нежели со сложением. Отчасти это связано со свойствами данных математических операций.

Всем известно, что от перемены мест слагаемых значение суммы не меняется. В вычитании же всё гораздо сложней. Если поменять числа местами, получится совершенно другой результат.

Схожим свойством в прибавлении и убавлении является то, что нулевой элемент не меняет исходное число.

В вычитании всё относительно просто, если первое число больше второго, однако в школе будут рассматриваться и противоположные примеры. В этом случае возникает понятие отрицательного числа.

Например, если нужно вычесть из 5 число 2, то всё несложно. 5-2=3, таким образом разность числа составит 3. Однако, что делать, если необходимо посчитать, сколько будет два минус пять?

В выражении 2-5 разность уйдет в минус, то есть в отрицательное значение. Из двойки легко можно вычесть двойку, получив таким образом ноль, однако от пятерки остается ещё три. Таким образом, результатом данного выражения будет отрицательное число три. То есть, 2-5=-3.

Что такое разность чисел: уменьшаемое, вычитаемое, разность — правило

Статья познакомит читателя с понятиями «разность чисел», «вычитаемое» и «уменьшаемое».

В арифметике существует всего четыре основных действия, которые мы называем сложением, умножением, вычитанием и делением.

Такие действия являются основой всей математики – они позволяют нам осуществлять все вычисления: как простые, так и самые сложные.

Самыми простыми действиями считаются сложение и вычитание, которые противоположны друг другу. Правда, слово «сложение» мы также используем и в обычной жизни.

Мы можем встретить фразу «сложить усилия, например, когда нам нужно сделать какую-нибудь работу всем вместе. Но вот с термином «вычитание» дело обстоит немного сложнее, и в разговоре оно встречается реже.

Мы редко услышим такие выражения, как «уменьшаемое», «вычитаемое», «разность». Но в сегодняшней статье мы подробно поговорим о них с точки зрения математики.

Что значит число уменьшаемое, число вычитаемое и разность чисел?

Что значит число уменьшаемое, число вычитаемое и разность чисел? Как известно, многие научные термины и выражения взяты из других языков, чаще греческого и латинского. Но те слова, которые будут рассмотрены ниже, имеют русское происхождение, потому нам будет проще их разобрать.

Например, что можно сказать о разности чисел? Если мы обратим внимание на корень слова «разность», то нам представится, например, его однокоренное слово «разница».

А если речь идет о математике, то тут и думать нечего – слово «разность» означает разницу между какими-то цифрами, а точнее, двумя числами.

Разница нам показывает, насколько одна величина больше другой или, наоборот, вторая меньше первой. Строго в математике это выглядит как результат вычитания.

Сразу же приведем пример. Допустим, буфетчица несет на подносе восемь пирожков. Пять из них она раздала посетителям. Сколько пирожков останется у буфетчицы на подносе? Если из 8 вычесть 5, то получится — 3. Теперь запишем это математически:

То есть разница между восемью и пятью – это три. Теперь нам понятно, что такое термин «разница».

Внимание: Если два числа равны друг другу, то разницы между ними не существует, она равна нулю (8 – 8 = 0).

Теперь нам следует выяснить, что такое вычитаемое и уменьшаемое. Снова представим значение слов по их смыслу. Чем может являться число уменьшаемое? Уменьшаемое – это то число, которое уменьшается при вычитании. От этого числа отнимают другое число. А что такое вычитаемое? Вычитаемым как раз и является том числом, которые мы отнимаем от уменьшаемого.

Вернемся к примеру с буфетчицей. Мы помним, как от восьми отнимали пять, и у нас получилось три. Мы выяснили, что тройка является разницей между двумя этими числами. Теперь нам уже не сложно понять, что 8 – это число уменьшаемое, а 5 – это число вычитаемое.

Как найти уменьшаемое и вычитаемое число?

Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:

• Y – 10 = 18, где Y – число уменьшаемое
• Значит, Y = 18 + 10
• 18 + 10 = 28
• Y = 28

Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:

• 28 – B = 10, где B – число вычитаемое
• Значит, B = 28 – 10
• 28 – 10 = 18
• B = 18

Что такое разность чисел в математике и как найти разность чисел

В этой статье мы рассмотрим, что такое разность чисел в математике, и как человеку, интересующемуся этой наукой, найти разность чисел.

Что такое разность чисел в математике

Вычитание является одной из 4 арифметических операций. Для его обозначения служит математический знак «−» (минус). Вычитание противоположно по смыслу операции сложения.

Операция вычитания в общем случае записывается следующим образом:

A − B = C

Число Математическое название

A	Уменьшаемое
B	Вычитаемое
C	Разность чисел

Пример: 6 − 2 =4

Здесь разностью чисел будет являться число 4. Следовательно, разность между любыми числами A и B это такое число C, которое при прибавлении к B даст в сумме A (4 при прибавлении к 2 дает 6 — значит, 4 это разность 6 и 2).

Как найти разность чисел

Уже из самого определения следует, как вычислить разность между двумя числами. При небольших числах можно делать это в уме. Детей в начальной школе учат следующим образом. Представьте, что у Вас есть 5 яблок, и 3 из них забрали. Сколько у Вас осталось? Правильно — 2 яблока. Постепенно Вы доведете вычисления до автоматизма и будете сразу выдавать ответ.

Однако для чисел выше 50 такое наглядное представление перестает работать. Большое количество предметов тяжело представить в уме, поэтому здесь на помощь приходит другой способ:

Вычисление разности в столбик

Школьники изучают этот способ в рамках курса математики, обычно во втором или третьем классе. Взрослые люди, пользующиеся калькулятором, зачастую забывают, как считать в столбик. Однако калькулятор не всегда бывает под рукой. Освежите в памяти школьные знания, посмотрев это видео.

Вычисление разности в столбик – видео

Этот способ применим и тогда, когда Вам нужно вычесть большее число из меньшего. В реальной жизни такое обычно не требуется, но может пригодиться при решении математических задач.

Допустим, в примере A − B = C B больше, чем A. Тогда C будет отрицательным. Чтобы вычислить разность, «разверните» пример: посчитайте значение B − A.

Когда Вы закончите считать эту разность, у вас получится число C, только с противоположным знаком: оно будет больше нуля. Чтобы завершить вычисления, припишите к нему спереди знак минус.