Кинематика

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах [с].
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Путь — вектор, проведенный из начальной точки пути в конечную [м].

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

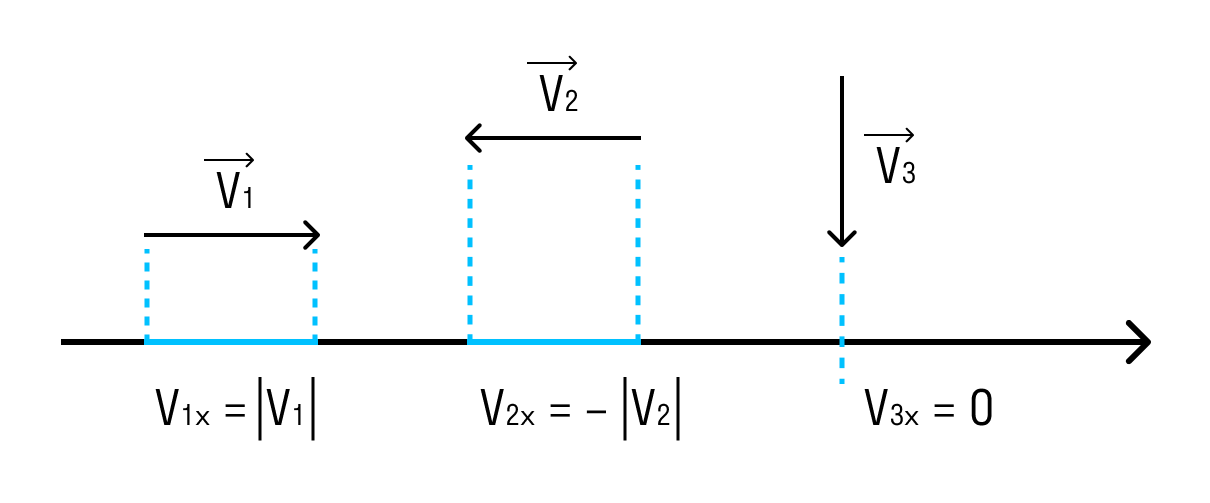
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости

V ср.путевая = S/t

Подставим значения:

V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уравнение движения

Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v &lt, 0), и тогда уравнение движения принимает вид:

Графики

Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.

В видео ниже я рассказываю, как строить графики кинематических величин и зачем они нужны.

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

То есть прямолинейное движение — это движение с ускорением по прямой линии, движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела в данный момент времени. У равноускоренного движения в уравнении

Для данного процесса также важно уметь находить конечную скорость. Это часто упрощает решение задач. Она находится по формуле

Задача

Найдите местоположение автобуса через 0,5 часа после начала движения, разогнавшегося до скорости 60 км/ч за 3 минуты.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

v = v0 + at

a = v — v0 / t

Так как автобус двигался с места, v0 = 0. Значит

a = v/t

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:

a = v/t = 60/0,05 = 1200 км/ч^2

Теперь возьмем уравнение движения.

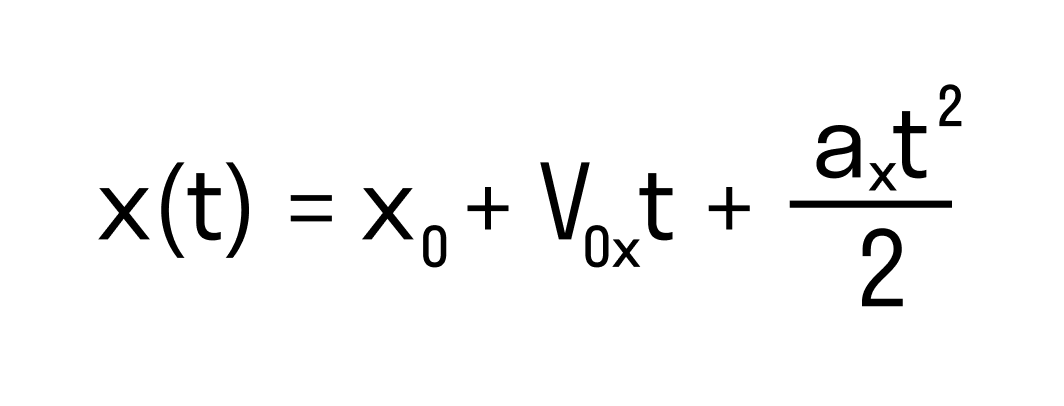
Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

x(t) = axt^2/2

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:

x = 1200*0,5^2/2 = (1200*0,5^2)/2 = 150 км

Ответ: через полчаса координата автобуса будет равна 150 км.

Графики

Мы уже знаем, что такое графики функций и зачем они нужны. Для прямолинейного равноускоренного движения графики будут отличаться. Об этом — в видео ниже.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с^2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с^2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с^2.

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела, когда тело движется вокруг некоторой точки. Очень важно разделить движение по окружности и вращение тела.

При вращательном движении тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.

Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги. Это очень похоже на равномерное движение, только в данном случае мы имеем дело с дугами.

При движении по окружности тело двигается вокруг одной точки, а при вращении — все точки тела движутся вокруг оси вращения.

В видеролике ниже рассказано про ускорение при криволинейном движении. Оно складывается из двух составляющих — нормальной и тангенциальной. При равномерном движении по окружности тангенциальная составляющая отсутствует, остается нормальная, которую мы в данном случае называем центростремительной.

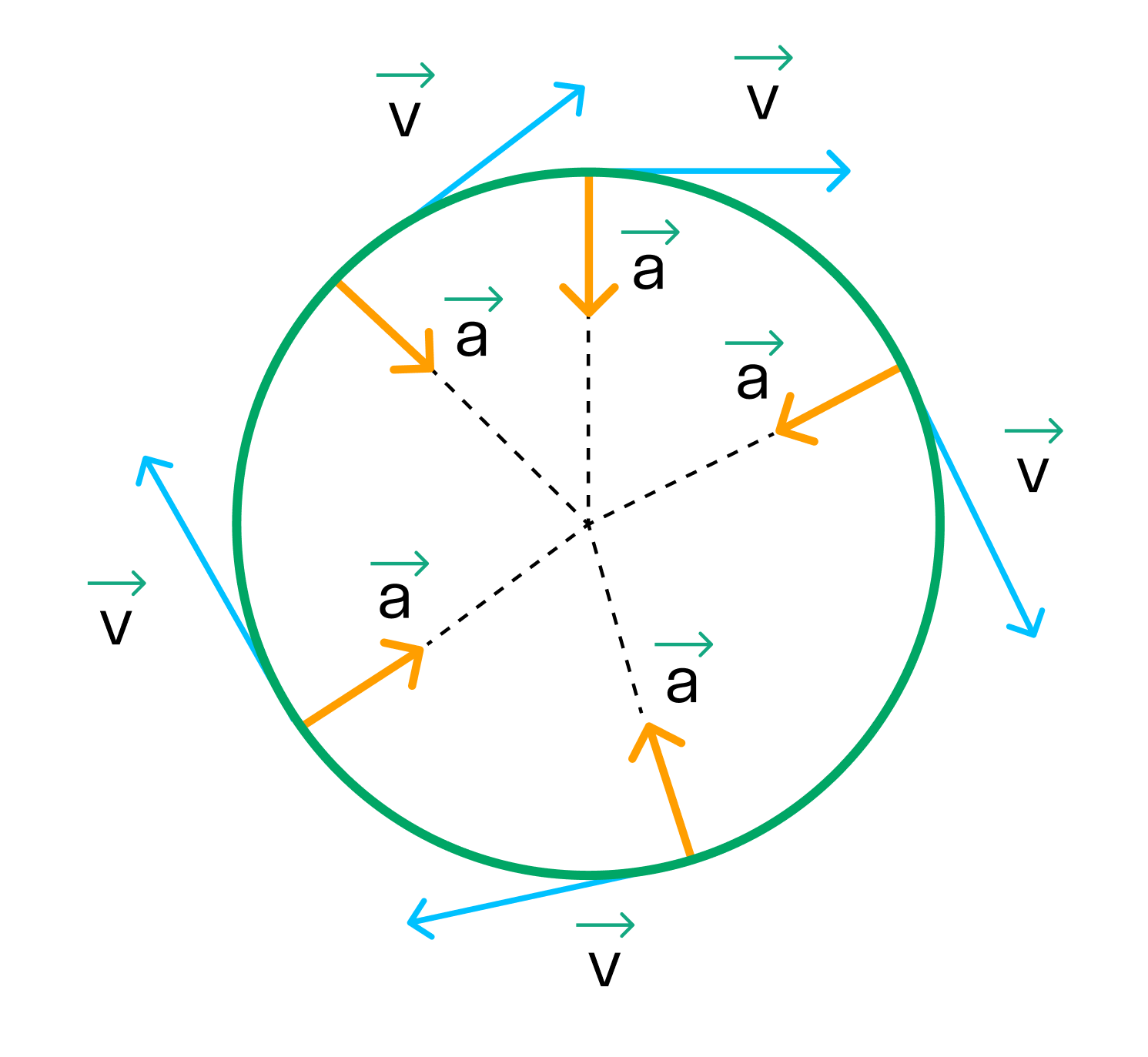
Центростремительное ускорение

При движении по окружности модуль скорости постоянен, а вот направление скорости постоянно меняется. За изменение направления скорости отвечает центростремительное ускорение.

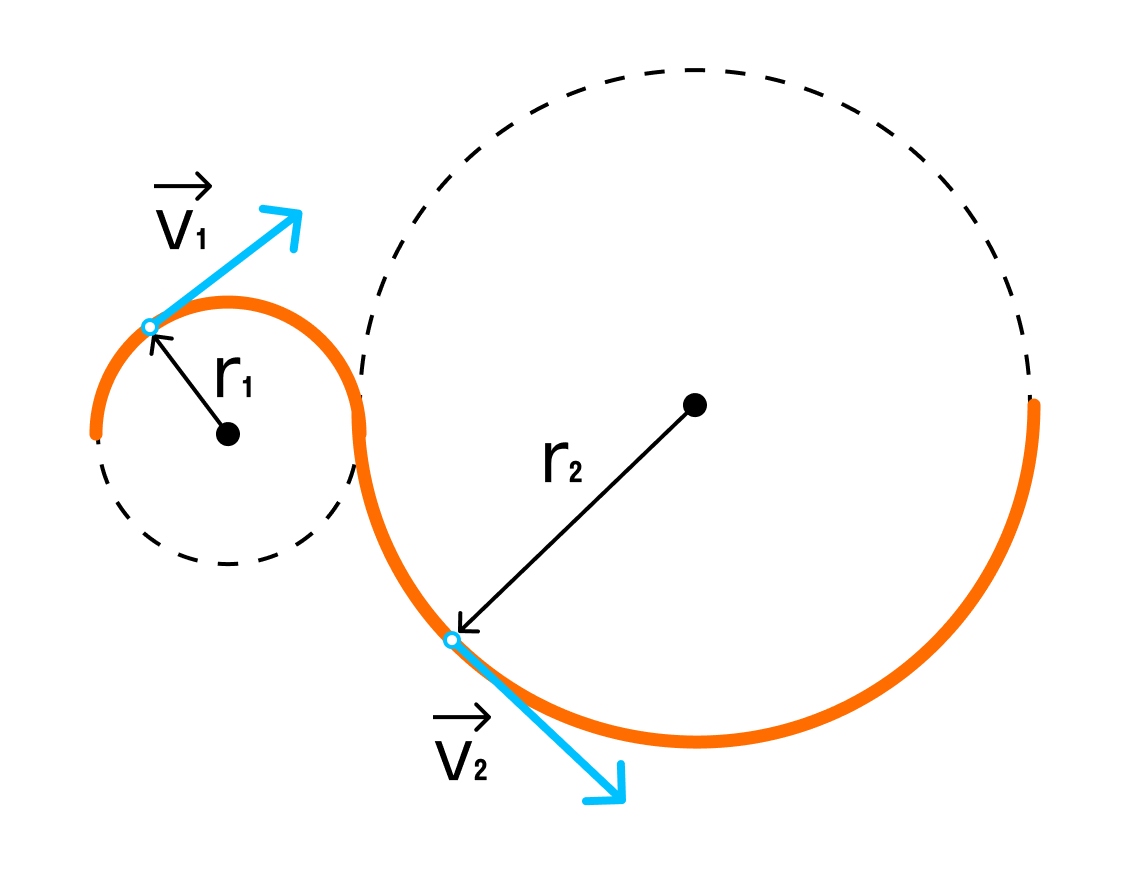
Задачка

Мотоцикл движется по закруглённому участку дороги радиусом 120 м со скоростью 36 км/ч. Чему равно центростремительное ускорение мотоцикла?

Решение:

Возьмем формулу центростремительного ускорения тела

aц = v^2/R

В условии задачи скорость дана в километрах в час, а радиус в метрах. Значит, нужно перевести скорость в м/с, чтобы избежать коллапса в решении.

36 км/с = 10 м/с

Теперь можно подставить значения в формулу:

aц = 10^2/120 = 100/120 = 10/12 ≃ 0,83 м/с^2

Ответ: центростремительное ускорение мотоциклиста равно 0,83 м/с^2

Движение — один из природных феноменов, которые изучает  отдельный раздел физики. Название «кинематика» происходит от греческого слова κινειν, которое в переводе означает движение, а звучит это слово как «киней». Основные понятия кинематики — это:

• материальная точка,
• физическое тело,
• пространство,
• время,
• координата,
• ускорение,
• скорость,
• перемещение,
• путь.

Можно увидеть, что здесь нет таких распространенных терминов, как сила, воздействие, взаимодействие. Это предмет изучения другого раздела физики — динамики. А основная задача кинематики — найти положение тела в пространстве в заданный момент времени. Кинематика — это идеализированный раздел физики, который изучает движение в чистом виде, без определения причин, его вызывающих. Используются средства геометрии, алгебры, математического анализа, дифференциального и интегрального исчисления.

В своем большинстве определения и формулы кинематики носят теоретический характер, но создают прочную основу для реального определения характеристик движения конкретного тела. Если искать ответ на вопрос, что изучает кинематика, то наиболее правильным ответом будет — как движутся физические тела. Почему это происходит — предмет других разделов механики.

Для начала уточним, что в кинематике все измерения и вычисления производятся в пределах системы измерения СИ (SI). При изучении движения нас интересует только несколько величин из довольно широкой таблицы. Это масса, расстояние (длина) и время. Соответственно, единицами измерения становятся килограмм (кг), метр (м) и секунда (с). Угол измеряется не в градусах, а в радианах (рад).

В условиях задачи могут использоваться производные и внесистемные единицы, например, километр, тонна, час. Но при записи условия задачи необходимо перейти к стандартным системным величинам, преобразовав исходные данные. Сделать это несложно, например:

• 1 час — 3600 с,
• 1 тонна — 1000 кг, или 1 ∙103,
• 1 километр — 1000м, или 1 ∙103м,
• 1 сантиметр — 0,01 м, или 1 ∙ 10-2м.

Все ответы в задачах должны быть указаны только в системных единицах и стандартной записи числа (а ∙ 10n, n- целое число).

При вычислениях можно пользоваться только величинами одного размерного ряда, например, умножать, делить, вычитать только километры с километрами, секунды с секундами и т.д. Для упрощения перевода единиц можно воспользоваться таблицей:

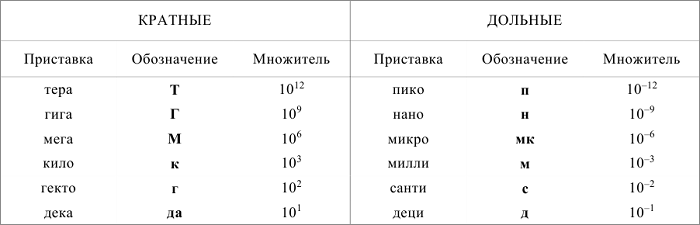
Но есть один нюанс, в некоторых задачах ЕГЭ дополнительно указано, в каких единицах представить результат. Всегда дочитывайте задание до конца. Если там указано, что нужно записать ответ в км/час, то м/с могут быть засчитаны как ошибка, даже если все формулы написаны правильно, а вычисления сделаны точно.

Расшифровка основных понятий кинематики

Материальная точка — движущееся, или неподвижное тело, размеры которого ничтожно малы по сравнению с расстояниями. Например, исследуя движение самолета из Москвы во Владивосток, или Санкт-Петербург, его можно считать материальной точкой. Длина и размах крыльев намного меньше, чем длина пути. А вот при перемещении того же самолета из ангара на взлетную полосу, размеры и длина пути одного порядка, термин использовать нельзя.

Система отсчета (СО) — координатная сеть, в которой мы изучаем поведение материальной точки. В СО входят тело отсчета, привязанные к нему  оси координат, часы и средства измерения длины. Телом отсчета выбирается предмет, или сооружение, которые заведомо неподвижны в данной системе. Например, исследуя движение того же самолета, за тело отсчета можно принять диспетчерскую башню, или вышку наземного флюгера. Координата тела отсчета (0,0). Начальное положение движущегося тела (точка старта) обозначается как А (X0,Y0).

Движение каждой материальной точки можно изобразить линией, которая получила название траектория. Линия может быть прямой, ломаной, дугообразной. Если тело движется по прямой, то движение называют прямолинейным. Каждую ломаную и дугу можно разбить на мелкие участки, которые приближенно считаются прямыми.

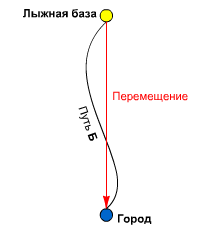
В кинематике используются два понятия, которые часто путают — путь и перемещение. Путаницу усугубляет то, что измеряются они в одинаковых единицах, метрах. Но физическая суть их отличается:

• путь — длина траектории,
• перемещение — кратчайшее расстояние между точками начала и конца пути.

Если тело движется по замкнутому кругу, то путь равен периметру получившейся фигуры, а перемещение равно нулю. Формула для определения пути при равномерном движении:

S= v ∙t, где v — скорость движения, а t – время движения. Путь величина скалярная, то есть, от направления не зависит. Перемещение определяется как вектор, с началом в точке старта и концом в точке финиша. Путь и перемещение совпадают только при прямолинейном движении в одной системе отсчета.

Скорость — векторная величина, показывающая какое расстояние проходит тело за единицу времени. Измеряется в м/с, определяется по формуле:

V=S\t. Это средняя скорость, для определения которой Если тело двигалось с разными скоростями на разных участках, то среднюю скорость нельзя рассчитывать, как среднее арифметическое. Это ошибка. Нужно длину всего пути разделить на все время движения.

Средняя скорость перемещения — рассчитывается по формуле:

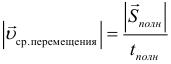
, где Sполн – перемещение, а не путь.

Ускорение — изменение скорости за единицу времени

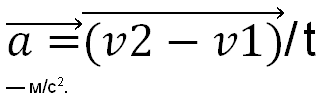
Единица измерения ускорения — м/с2.

Движение называется равноускоренным, если каждую секунду скорость увеличивается на одну и ту же величину. Перемещение при равноускоренном прямолинейном движении определяется по формуле:

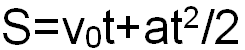
Если тело равномерно замедляется, то формула выглядит так:

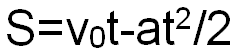
Координата (положение) тела в системе отсчета определяется формулой:

Это базовые формулы, из которых легко получить остальные, необходимые для вычисления координаты движущегося тела:

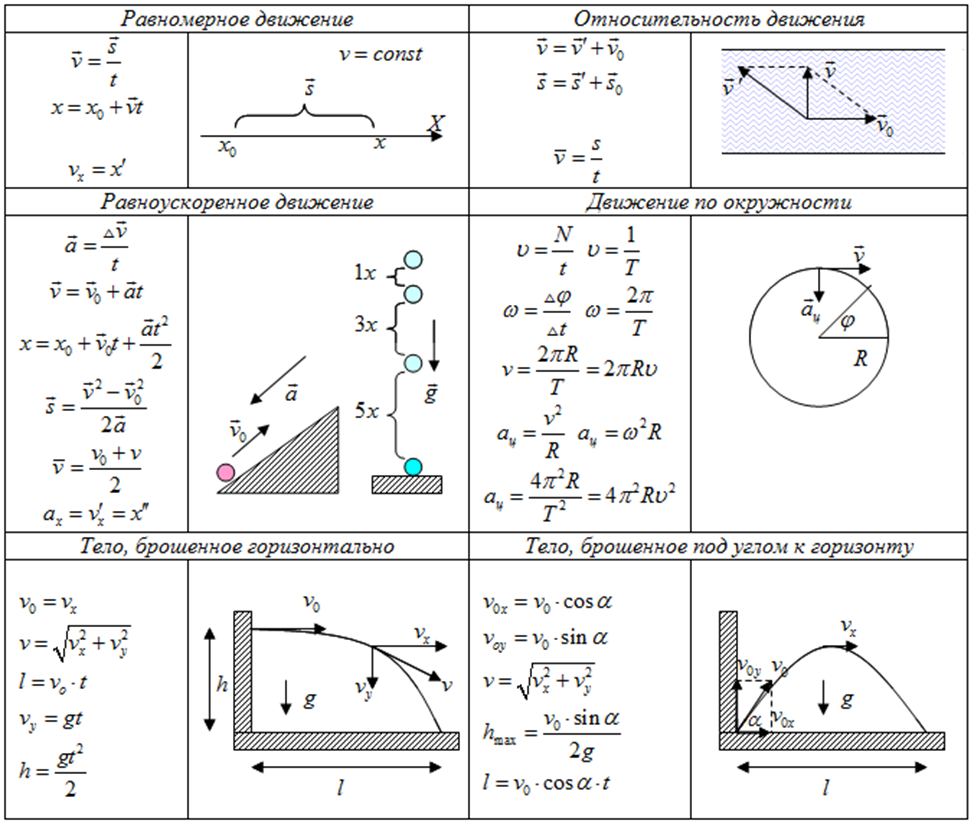
Если отдельно рассматривать движение падающего тела, то формулы отличаются только тем, что ускорение всегда одно и то же — g= 9,8 м/с2.

Рассмотренные формулы применимы в неподвижных системах отсчета, привязанных к одному телу. В движущихся системах координат все происходит значительно сложнее.